JAKARTA, studyinca.ac.id – Trigonometri adalah cabang matematika yang mempelajari hubungan antara sudut dan sisi segitiga, terutama segitiga siku-siku. Konsep ini sangat penting dalam berbagai bidang seperti fisika, teknik, navigasi, dan astronomi. Selain itu, trigonometri membantu kita memahami fenomena gelombang, rotasi, dan pergerakan. Dengan mempelajari trigonometri, seseorang dapat meningkatkan kemampuan analitis dan problem solving secara lebih mendalam.
Sejarah Trigonometri
Sejarah trigonometri bermula dari peradaban kuno, seperti Mesir dan Babilonia, yang menggunakan hubungan sisi dan sudut untuk keperluan arsitektur dan astronomi. Namun, trigonometri modern berkembang pesat oleh matematikawan Yunani, India, dan Arab. Hipparchus dianggap sebagai “Bapak Trigonometri” karena menyusun tabel pertama. Karena itu, trigonometri bukan hanya ilmu abstrak tetapi juga bagian dari sejarah ilmiah dunia.
Konsep Dasar Trigonometri
Trigonometri didasarkan pada hubungan sisi dan sudut dalam segitiga. Ada tiga fungsi dasar, yaitu sinus (sin), cosinus (cos), dan tangen (tan). Fungsi ini digunakan untuk menghitung panjang sisi atau besar sudut dalam segitiga. Selain itu, pemahaman konsep dasar ini menjadi fondasi untuk mempelajari fungsi lanjutan, identitas, dan persamaan.
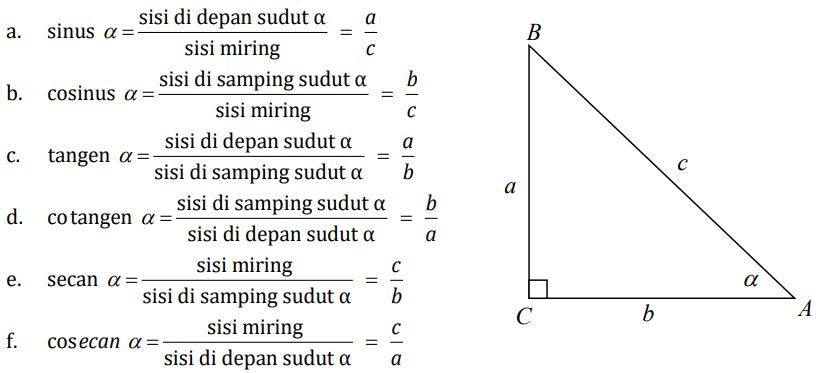
Segitiga Siku-Siku dan Fungsi Dasar
Segitiga siku-siku memiliki satu sudut 90 derajat. Dalam segitiga ini, sinus sudut didefinisikan sebagai perbandingan sisi depan dengan hipotenusa, cosinus sebagai perbandingan sisi samping dengan hipotenusa, dan tangen sebagai perbandingan sisi depan dengan sisi samping. Saya sendiri sering menggunakan segitiga siku-siku untuk menjelaskan fungsi dasar ini kepada siswa, dan mereka biasanya cepat memahami konsepnya karena visualisasinya sederhana. Karena itu, segitiga siku-siku menjadi pusat pembelajaran dasar.
Rumus Pythagoras dan Trigonometri
Selain itu, kombinasi rumus Pythagoras dan fungsi memudahkan penyelesaian masalah nyata, seperti pengukuran ketinggian bangunan atau menara.
Identitas Trigonometri Dasar
Identitas trigonometri adalah persamaan yang selalu benar untuk semua nilai sudut tertentu. Contohnya termasuk identitas fundamental seperti sin²θ + cos²θ = 1, dan identitas tangen seperti tanθ = sinθ / cosθ. Selain itu, identitas ini digunakan untuk menyederhanakan persamaan dan mempermudah perhitungan. Karena itu, penguasaan identitas trigonometri menjadi langkah penting bagi pemahaman lanjutan.
Fungsi Lanjutan
Selain sinus, cosinus, dan tangen, terdapat fungsi lanjutan seperti cosecan (csc), secan (sec), dan cotangen (cot). Fungsi-fungsi ini merupakan kebalikan dari fungsi dasar dan sering digunakan dalam berbagai soal matematika. Selain itu, mereka berguna dalam analisis gelombang dan perhitungan sudut dalam bidang teknik. Karena itu, memahami fungsi lanjutan memperluas kemampuan analitis siswa.
Sudut Istimewa dan Nilainya
Sudut istimewa seperti 0°, 30°, 45°, 60°, dan 90° memiliki nilai sinus, cosinus, dan tangen yang sering digunakan. Menghafal nilai-nilai ini memudahkan perhitungan cepat dalam soal matematika dan fisika. Selain itu, pemahaman sudut istimewa membantu menyelesaikan soal tanpa harus menggunakan kalkulator. Karena itu, latihan soal dengan sudut istimewa sangat disarankan.
Aplikasi dalam Kehidupan Sehari-Hari
Trigonometri tidak hanya ada di buku pelajaran. Konsep ini digunakan dalam arsitektur untuk menghitung kemiringan atap, dalam navigasi untuk menentukan posisi kapal atau pesawat, dan dalam astronomi untuk mengukur jarak bintang. Saya sendiri menggunakan sederhana ketika mencoba memperkirakan tinggi pohon di halaman rumah tanpa harus memanjatnya. Karena itu, menjadi ilmu yang aplikatif dan relevan.
Trigonometri dalam Fisika
Trigonometri mendukung berbagai konsep fisika, termasuk gerak harmonik, gelombang, dan gaya. Fungsi sinus dan cosinus digunakan untuk mendeskripsikan gerakan periodik, sedangkan tangen sering muncul dalam analisis vektor. Selain itu, pemahaman membantu menyelesaikan masalah fisika dengan tepat dan efisien. Karena itu, siswa fisika sangat bergantung pada konsep .
Teknik
Bidang teknik, seperti teknik sipil, mesin, dan elektro, memanfaatkan trigonometri untuk desain dan analisis. Contohnya, perhitungan sudut kemiringan, gaya pada struktur, atau medan listrik sering menggunakan fungsi . Selain itu, membantu membuat perhitungan akurat dan desain yang aman. Karena itu, kemampuan menjadi syarat penting dalam pendidikan teknik.
Persamaan Trigonometri
Persamaan trigonometri adalah persamaan yang mengandung fungsi trigonometri. Penyelesaian persamaan ini membutuhkan strategi tertentu, termasuk penggunaan identitas dan grafik. Selain itu, persamaan menjadi dasar untuk soal ujian matematika dan aplikasi nyata. Karena itu, latihan soal persamaan membantu meningkatkan kemampuan analisis dan logika.
Gelombang
Konsep gelombang, termasuk gelombang air, bunyi, dan cahaya, menggunakan fungsi trigonometri untuk deskripsinya. Sinus dan cosinus menggambarkan amplitudo dan fase gelombang. Selain itu, analisis gelombang menggunakan membantu memahami fenomena fisika dan teknologi. Karena itu, menjadi jembatan antara matematika murni dan sains terapan.
Tips Mudah Belajar
Belajar trigonometri membutuhkan pemahaman konsep dan latihan rutin. Mulailah dengan fungsi dasar, segitiga siku-siku, dan identitas sederhana. Selain itu, visualisasi grafik dan praktik soal nyata membantu memperkuat pemahaman. Saya sendiri menyarankan menggunakan alat bantu visual seperti gambar dan diagram untuk mempermudah proses belajar. Karena itu, konsistensi dan latihan menjadi kunci menguasai .
Pentingnya Trigonometri
Dari pembahasan di atas, jelas bahwa trigonometri adalah cabang matematika yang esensial untuk sains, teknik, dan kehidupan sehari-hari. Selain itu, pemahaman fungsi, identitas, grafik, dan aplikasi praktis menjadi kunci keberhasilan belajar trigonometri. Saya yakin, siapa pun yang memahami dengan baik akan lebih mudah menyelesaikan masalah matematika, fisika, dan teknik secara efektif.
Temukan informasi lengkapnya Tentang: Pengetahuan
Baca Juga Artikel Berikut: Vulkanologi: Ilmu tentang Gunung Berapi dan Aktivitas Vulkanik

