Fungsi Eksponensial : Panduan Lengkap dan Aplikasinya

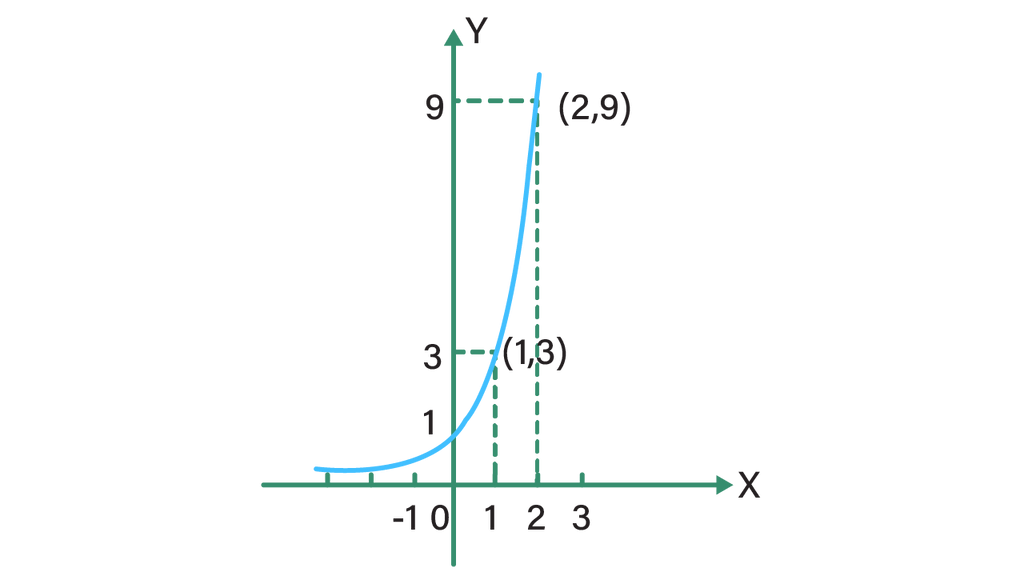
JAKARTA, studyinca.ac.id – Fungsi eksponensial adalah fungsi matematika yang memiliki variabel pada pangkat, misalnya f(x)=axf(x) = a^xf(x)=ax dengan $a>0$ dan a≠1a \neq 1a=1. Fungsi ini memiliki karakteristik unik, yaitu pertumbuhan yang sangat cepat jika $a>1$ dan penurunan yang cepat jika $0<a<1$.

Fungsi eksponensial banyak muncul dalam kehidupan sehari-hari, seperti pertumbuhan populasi, bunga bank, atau peluruhan radioaktif. Dengan memahami konsep ini, kita dapat menghitung perubahan yang terjadi secara cepat dan akurat.

Karakteristik Fungsi Eksponensial

Ada beberapa karakteristik penting dari fungsi eksponensial:

• Grafik selalu positif jika $a>0$.

• Titik potong dengan sumbu y terjadi di $y=1$.

• Memiliki asymptote horizontal di y = 0.

• Pertumbuhan atau penurunan bergantung pada nilai basis $a$.

Dengan karakteristik ini, kita dapat memprediksi perilaku fungsi eksponensial dengan lebih mudah tanpa harus menggambar grafik secara lengkap.

Pengenalan Fungsi Logaritma

Fungsi logaritma merupakan invers dari fungsi eksponensial. Secara matematis, y=log⁡axy = \log_a xy=loga​x jika dan hanya jika ay=xa^y = xay=x, dengan $a>0$ dan a≠1a \neq 1a=1.

Fungsi logaritma banyak digunakan untuk memecahkan persamaan eksponensial, menghitung pertumbuhan berbasis waktu, dan menganalisis data skala besar, misalnya dalam ilmu statistik atau ekonomi.

Hubungan Antara Eksponensial dan Logaritma

Fungsi eksponensial dan logaritma saling berkaitan erat. Jika y=axy = a^xy=ax, maka inversnya adalah x=log⁡ayx = \log_a yx=loga​y. Dengan kata lain, logaritma membantu kita “membalikkan” proses eksponensial.

Selain itu, logaritma memudahkan perhitungan angka yang sangat besar atau kecil, sehingga sering digunakan dalam komputasi dan analisis data. Misalnya, logaritma digunakan untuk menghitung tingkat pertumbuhan investasi tahunan yang eksponensial.

Sifat-Sifat Fungsi Eksponensial dan Logaritma

Ada beberapa sifat penting yang harus diketahui:

Fungsi Eksponensial:

• am⋅an=am+na^m \cdot a^n = a^{m+n}am⋅an=am+n

• aman=am−n\frac{a^m}{a^n} = a^{m-n}anam​=am−n

• (am)n=amn(a^m)^n = a^{mn}(am)n=amn

Fungsi Logaritma:

• log⁡a(xy)=log⁡ax+log⁡ay\log_a (xy) = \log_a x + \log_a yloga​(xy)=loga​x+loga​y

• log⁡axy=log⁡ax−log⁡ay\log_a \frac{x}{y} = \log_a x – \log_a yloga​yx​=loga​x−loga​y

• log⁡a(xn)=n⋅log⁡ax\log_a (x^n) = n \cdot \log_a xloga​(xn)=n⋅loga​x

Sifat-sifat ini memudahkan manipulasi persamaan eksponensial dan logaritma untuk menemukan solusi dengan cepat.

Cara Menyelesaikan Persamaan Eksponensial

Untuk menyelesaikan persamaan eksponensial, biasanya kita melakukan langkah-langkah berikut:

1. Samakan basis jika memungkinkan. Misalnya, 2x=82^x = 82x=8 → 2x=232^x = 2^32x=23 → $x=3$.

2. Jika basis berbeda, gunakan logaritma. Contoh: 3x=203^x = 203x=20 → x=log⁡320=ln⁡20ln⁡3x = \log_3 20 = \frac{\ln 20}{\ln 3}x=log3​20=ln3ln20​.

3. Gunakan sifat eksponensial untuk menyederhanakan persamaan kompleks.

Metode ini memudahkan kita menyelesaikan berbagai persamaan eksponensial dengan cepat.

Cara Menyelesaikan Persamaan Logaritma

Persamaan logaritma dapat diselesaikan dengan langkah-langkah berikut:

1. Gunakan sifat logaritma untuk menggabungkan atau memecah logaritma.

2. Ubah ke bentuk eksponensial. Misalnya, log⁡2x=3\log_2 x = 3log2​x=3 → 23=x2^3 = x23=x → $x=8$.

3. Periksa domain, karena logaritma hanya didefinisikan untuk bilangan positif.

Dengan strategi ini, penyelesaian persamaan logaritma menjadi lebih sistematis dan bebas dari kesalahan.

Fungsi Eksponensial dalam Kehidupan Sehari-hari

Fungsi eksponensial muncul di berbagai aspek kehidupan:

• Pertumbuhan Populasi: Populasi manusia atau hewan meningkat secara eksponensial dalam kondisi ideal.

• Bunga Bank: Bunga majemuk mengikuti fungsi eksponensial karena penghitungan bunga dilakukan berkali-kali.

• Peluruhan Radioaktif: Radioaktif atom tertentu menurun sesuai fungsi eksponensial negatif.

Dalam salah satu paragraf ini, perlu dicatat bahwa memahami konsep ini membantu kita membuat perencanaan keuangan, kesehatan, dan lingkungan dengan lebih baik.

Fungsi Logaritma dalam Ilmu dan Teknologi

Logaritma banyak diterapkan dalam ilmu pengetahuan dan teknologi, contohnya:

• Skala Richter untuk mengukur gempa bumi.

• Skala pH untuk mengukur keasaman atau kebasaan suatu larutan.

• Ilmu Komputer untuk analisis kompleksitas algoritma dan kompresi data.

Fungsi logaritma memudahkan kita mengelola data besar dan skala yang sulit dihitung secara langsung.

Logaritma Natural dan Basis Eksponensial e

Basis eksponensial $e\approx 2.718$ sangat penting dalam kalkulus, ekonomi, dan fisika. Logaritma natural $\ln x$ adalah logaritma dengan basis e.

Penggunaan $e$ memudahkan perhitungan pertumbuhan kontinu, misalnya bunga bank tahunan yang dihitung setiap detik, atau pertumbuhan populasi secara konstan.

Grafik Fungsi Eksponensial dan Logaritma

Grafik eksponensial selalu naik jika $a>1$ dan turun jika $0<a<1$. Sementara grafik logaritma meningkat secara perlahan untuk $x>1$.

Mengetahui bentuk grafik membantu kita memahami perilaku fungsi, menentukan solusi persamaan, dan memprediksi hasil perhitungan eksponensial atau logaritma.

Transformasi dan Perubahan Skala

Fungsi eksponensial dan logaritma dapat ditransformasi:

• Translasi: menggeser grafik ke atas, bawah, kiri, atau kanan.

• Refleksi: memantulkan grafik terhadap sumbu x atau y.

• Skala: memperbesar atau memperkecil grafik secara vertikal atau horizontal.

Transformasi ini penting ketika menganalisis data atau menyelesaikan soal yang memerlukan visualisasi.

Fungsi Eksponensial dan Logaritma dalam Ekonomi

Dalam ekonomi, fungsi ini digunakan untuk:

• Menghitung pertumbuhan investasi atau keuntungan.

• Analisis inflasi dan depresiasi aset.

• Model konsumsi dan produksi yang meningkat atau menurun secara eksponensial.

Dengan memahami konsep ini, analis ekonomi bisa membuat prediksi lebih akurat.

Kesalahan Umum dalam Menggunakan Fungsi Eksponensial dan Logaritma

Beberapa kesalahan yang sering terjadi:

• Tidak memperhatikan domain logaritma (harus > 0).

• Salah menulis basis eksponensial atau logaritma.

• Mengabaikan sifat logaritma saat menyederhanakan persamaan.

• Lupa memeriksa hasil akhir setelah substitusi.

Kesalahan ini bisa dihindari dengan latihan rutin dan pemahaman konsep yang mendalam.

Pentingnya Fungsi Eksponensial dan Logaritma

Fungsi eksponensial dan logaritma adalah dasar matematika yang sangat penting. Mereka tidak hanya relevan di sekolah atau kampus, tetapi juga dalam kehidupan sehari-hari, ilmu pengetahuan, dan teknologi.

Dengan pemahaman yang tepat, kita bisa menyelesaikan persamaan kompleks, menganalisis data, dan membuat keputusan yang lebih cerdas dalam berbagai bidang, mulai dari ekonomi hingga teknologi.

Temukan informasi lengkapnya Tentang:  Pengetahuan

Baca Juga Artikel Berikut: Vektor Matematika Dasar: Panduan Lengkap untuk Pemula