JAKARTA, studyinca.ac.id – Dalam dunia matematika, bangun ruang menjadi salah satu konsep penting yang mempelajari bentuk tiga dimensi. Jika bangun datar hanya memiliki panjang dan lebar, maka bangun ruang memiliki panjang, lebar, dan tinggi, sehingga dapat dihitung volumenya.
Bangunruang hadir di sekitar kita dalam kehidupan sehari-hari — dari bentuk rumah, bola sepak, hingga kemasan minuman. Dengan memahami konsep bangunruang, seseorang dapat menghubungkan teori matematika dengan realitas fisik di dunia nyata.
Secara umum, bangunruang juga disebut sebagai geometri ruang, yaitu cabang matematika yang mempelajari bentuk, ukuran, posisi, dan sifat dari objek tiga dimensi.
Ciri-Ciri Umum Bangun Ruang
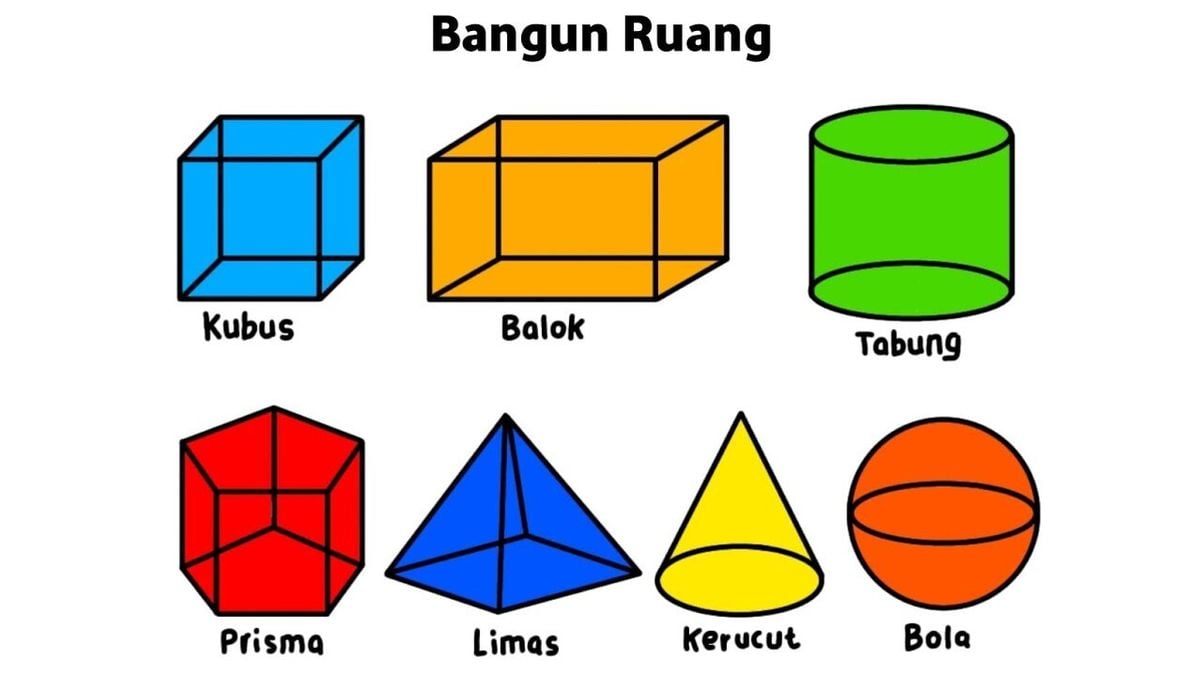
Agar lebih mudah dikenali, berikut beberapa ciri khas dari bangun ruang:
-
Memiliki volume (isi).
Berbeda dengan bangun datar, bangunruang mampu menampung sesuatu di dalamnya. -
Memiliki sisi, rusuk, dan titik sudut.
-
Sisi: bidang yang membentuk permukaan bangun ruang.
-
Rusuk: garis pertemuan antara dua sisi.
-
Titik sudut: titik pertemuan antara beberapa rusuk.
-
-
Mempunyai bentuk tiga dimensi.
Artinya, bisa dilihat dari berbagai sisi — depan, samping, dan atas. -
Dapat dihitung volume dan luas permukaannya.
Volume menunjukkan isi dari bangun tersebut, sementara luas permukaan menunjukkan seberapa besar area luarnya.
Jenis-Jenis Bangun Ruang
Secara umum, bangun ruang dibagi menjadi dua kelompok besar, yaitu bangun ruang sisi datar dan bangun ruang sisi lengkung. Keduanya memiliki karakteristik dan rumus berbeda.
Bangun Ruang Sisi Datar
Bangun ruang sisi datar adalah bentuk tiga dimensi yang seluruh sisinya berupa bidang datar. Contohnya: kubus, balok, prisma, dan limas.
1. Kubus
Kubus adalah bangun ruang dengan enam sisi berbentuk persegi yang sama besar. Setiap rusuknya memiliki panjang yang sama.
Contoh di dunia nyata: dadu, kotak kado, atau rubik.
Ciri-ciri kubus:
-
Jumlah sisi: 6
-
Jumlah rusuk: 12
-
Jumlah titik sudut: 8
Rumus kubus:
-
Volume = s³
-
Luas permukaan = 6 × s²
2. Balok
Balok mirip dengan kubus, namun memiliki panjang, lebar, dan tinggi yang berbeda.
Contoh di dunia nyata: kotak tisu, kardus, atau lemari.
Ciri-ciri balok:
-
Jumlah sisi: 6 (berbentuk persegi panjang)
-
Jumlah rusuk: 12
-
Jumlah titik sudut: 8
Rumus balok:
-
Volume = p × l × t
-
Luas permukaan = 2 × (pl + pt + lt)
3. Prisma
Prisma adalah bangun ruang yang memiliki dua bidang sejajar berbentuk sama, sementara sisi lainnya berbentuk persegi panjang.
Contoh di dunia nyata: atap rumah, tenda segitiga.
Rumus prisma:
-
Volume = luas alas × tinggi
-
Luas permukaan = (2 × luas alas) + (keliling alas × tinggi)
4. Limas
Limas adalah bangun ruang dengan alas berupa bangun datar (persegi, segitiga, atau segiempat), sedangkan sisi lainnya berbentuk segitiga yang berkumpul pada satu puncak.
Contoh di dunia nyata: piramida di Mesir, tenda camping.
Rumus limas:
-
Volume = ⅓ × luas alas × tinggi
-
Luas permukaan = luas alas + jumlah luas sisi tegak
Bangun Ruang Sisi Lengkung
Jenis bangun ruang ini memiliki permukaan melengkung, seperti bola, tabung, dan kerucut.
1. Tabung
Tabung (silinder) memiliki dua sisi berbentuk lingkaran dan satu sisi melengkung yang menghubungkannya.
Contoh di dunia nyata: kaleng minuman, pipa air.
Rumus tabung:
-
Volume = π × r² × t
-
Luas permukaan = 2πr (r + t)
2. Kerucut
Kerucut memiliki alas berbentuk lingkaran dan sisi lengkung yang meruncing ke satu titik puncak.
Contoh di dunia nyata: topi ulang tahun, corong minyak.
Rumus kerucut:
-
Volume = ⅓ × π × r² × t
-
Luas permukaan = πr (r + s), dengan s = garis pelukis
3. Bola
Bola adalah bangunruang berbentuk sempurna, di mana seluruh titik pada permukaannya berjarak sama dari pusat.
Contoh di dunia nyata: bola basket, bola dunia.
Rumus bola:
-
Volume = ⅘ × π × r³
-
Luas permukaan = 4πr²
Anekdot Edukatif: Belajar Bangun Ruang dari Kehidupan Sehari-Hari
Seorang siswa SMA di Yogyakarta pernah bercerita, ia mulai memahami bangunruang bukan dari buku pelajaran, melainkan saat membantu ayahnya membuat kotak kayu. Saat mengukur panjang, lebar, dan tinggi, barulah ia sadar bahwa konsep matematika itu benar-benar nyata.
“Rasanya seperti menemukan pola di balik dunia,” katanya sambil tersenyum.
Cerita ini menunjukkan bahwa bangun ruang bukan sekadar teori abstrak, tetapi cara manusia memahami bentuk-bentuk di sekitarnya.
Pentingnya Mempelajari Bangun Ruang
Mengapa siswa harus memahami bangunruang? Jawabannya sederhana: karena konsep ini digunakan dalam banyak aspek kehidupan.
-
Dalam arsitektur dan desain.
Bangun ruang menjadi dasar perhitungan dalam membangun rumah, jembatan, hingga gedung pencakar langit. -
Dalam seni dan kriya.
Seniman menggunakan bentuk ruang untuk menciptakan karya tiga dimensi seperti patung, instalasi, dan model. -
Dalam teknologi dan sains.
Konsep volume dan bentuk tiga dimensi digunakan dalam perancangan robot, kendaraan, hingga simulasi komputer. -
Dalam kehidupan sehari-hari.
Menghitung isi air dalam botol, memilih ukuran kardus, atau menentukan kapasitas tangki — semuanya melibatkan pemahaman bangunruang.
Perbandingan Antara Bangun Datar dan Bangun Ruang
| Aspek | Bangun Datar | Bangun Ruang |
|---|---|---|
| Dimensi | 2 Dimensi (panjang & lebar) | 3 Dimensi (panjang, lebar, tinggi) |
| Volume | Tidak memiliki volume | Memiliki volume |
| Contoh | Persegi, segitiga, lingkaran | Kubus, balok, bola |
| Rumus Utama | Luas & keliling | Luas permukaan & volume |
| Visualisasi | Datar, hanya satu bidang | Dapat dilihat dari berbagai sisi |
Perbandingan ini memperjelas bahwa bangun ruang adalah perluasan konsep bangun datar ke dimensi yang lebih kompleks dan realistis.
Rumus Lengkap Bangun Ruang untuk Pembelajaran
Agar lebih mudah diingat, berikut tabel ringkas rumus bangunruang yang sering dipelajari di sekolah:
| Jenis BangunRuang | Volume | Luas Permukaan |
|---|---|---|
| Kubus | s³ | 6 × s² |
| Balok | p × l × t | 2(pl + pt + lt) |
| Prisma | Luas alas × tinggi | 2 × luas alas + keliling alas × tinggi |
| Limas | ⅓ × luas alas × tinggi | Luas alas + luas sisi tegak |
| Tabung | π × r² × t | 2πr (r + t) |
| Kerucut | ⅓ × π × r² × t | πr (r + s) |
| Bola | ⅘ × π × r³ | 4πr² |
BangunRuang dalam Konteks Pendidikan Modern
Di era pendidikan abad ke-21, bangun ruang tak lagi hanya diajarkan lewat rumus di papan tulis. Sekolah modern kini menggabungkan teknologi visual 3D, augmented reality, dan alat peraga digital untuk membantu siswa memahami bentuk tiga dimensi secara interaktif.
Misalnya, dengan aplikasi pembelajaran geometri, siswa bisa memutar model kubus atau kerucut dalam layar dan melihat bagaimana volume berubah ketika dimensi diperbesar.
Pendekatan ini membuat matematika terasa lebih nyata, menyenangkan, dan relevan dengan dunia digital masa kini.
Kesalahan Umum Saat Belajar BangunRuang
Meskipun terlihat sederhana, banyak siswa melakukan kesalahan dalam menghitung bangunruang. Beberapa di antaranya adalah:
-
Keliru membedakan tinggi dan sisi miring (pada kerucut).
-
Menggunakan satuan yang tidak konsisten (cm dan m).
-
Lupa mengalikan atau membagi dengan ⅓ untuk bangun berbentuk limas dan kerucut.
-
Tidak menuliskan satuan hasil (cm³ atau m³).
Menghindari kesalahan kecil ini akan membantu siswa memahami konsep ruang dengan lebih baik.
Keterkaitan Bangun Ruang dengan Kehidupan Sosial dan Teknologi
Menariknya, bangun ruang tidak hanya berfungsi dalam konteks akademis, tapi juga sosial. Dalam kehidupan masyarakat, pemahaman tentang bentuk dan volume berperan dalam desain perkotaan, pembangunan rumah layak huni, hingga perencanaan ruang publik.
Di dunia teknologi, bentuk-bentuk geometri ruang menjadi dasar desain grafis, game development, hingga permodelan arsitektur virtual. Dengan kata lain, belajar bangunruang juga berarti belajar memahami dunia tiga dimensi yang kita tinggali.
Anekdot: Ketika Matematika Bertemu Kreativitas
Seorang mahasiswa teknik arsitektur di Bandung pernah berkata, “Saya dulu tidak suka matematika, tapi begitu belajar bangun ruang, semuanya terasa hidup. Dari sana saya bisa membuat desain rumah impian saya sendiri.”
Ucapan itu menggambarkan bahwa bangunruang tidak hanya soal angka, tetapi juga tentang cara berpikir kreatif — bagaimana seseorang melihat dunia dari berbagai sudut pandang dan memadukan logika dengan imajinasi.
Kesimpulan: BangunRuang, Dasar dari Dunia Tiga Dimensi
Bangunruang bukan sekadar materi pelajaran matematika. Ia adalah fondasi untuk memahami bentuk, volume, dan struktur di dunia nyata. Dari kubus sederhana hingga bola kompleks, semua mengajarkan prinsip logika dan keseimbangan yang relevan untuk berbagai bidang kehidupan.
Memahami bangunruang berarti memahami cara dunia terbentuk — dari ruang di rumah, bentuk bangunan, hingga struktur molekul dalam sains. Maka, pelajaran ini tidak hanya penting bagi siswa, tetapi juga menjadi jembatan antara pengetahuan teori dan kehidupan praktis.
Baca juga konten dengan artikel terkait tentang: Pengetahuan
Baca juga artikel lainnya: Bangun Datar konsep dasar geometri pembentuk dunia belajar

