JAKARTA, studyinca.ac.id – Dalam dunia komputer dan jaringan, pengiriman data menjadi hal yang sangat penting. Namun, setiap kali data dikirim dari satu perangkat ke perangkat lain, selalu ada risiko terjadi kesalahan. Misalnya, gangguan listrik, noise pada saluran, hingga kerusakan media penyimpanan dapat membuat bit-bit data berubah tanpa sengaja. Oleh karena itu, kode Hamming hadir sebagai solusi untuk menemukan sekaligus memperbaiki kesalahan tersebut.
Bagi mahasiswa teknik informatika, sistem informasi, maupun teknik elektro, pemahaman tentang kode Hamming menjadi dasar penting dalam belajar sistem digital. Selain itu, artikel ini akan membahas secara lengkap mulai dari pengertian dasar, sejarah, cara kerja, hingga contoh soal yang mudah dipahami.
Pengertian Kode Hamming

Pada dasarnya, kode Hamming adalah metode untuk menemukan dan memperbaiki kesalahan data. Metode ini bekerja dengan cara menambahkan bit-bit tambahan pada data asli. Dengan demikian, sistem dapat mengetahui posisi bit yang salah dan langsung memperbaikinya secara otomatis.
Berbeda dengan metode sederhana seperti parity check yang hanya bisa menemukan kesalahan, kode Hamming punya kemampuan lebih. Artinya, ketika ada kesalahan pada satu bit, sistem bisa langsung menemukan lokasi kesalahan itu dan memperbaikinya. Jadi, tidak perlu meminta pengiriman ulang data.
Selain itu, dalam teori coding, kode Hamming masuk dalam golongan linear error-correcting code. Metode ini menggunakan konsep jarak Hamming untuk mengukur perbedaan antara dua deretan biner. Singkatnya, jarak Hamming dihitung dari jumlah posisi bit yang berbeda antara dua kode.
Sejarah Penemuan Kode Hamming
Kode Hamming pertama kali dibuat oleh Richard Wesley Hamming pada tahun 1950. Saat itu, ia bekerja di Bell Telephone Laboratories. Menariknya, penemuan ini lahir dari rasa frustasi Hamming ketika menggunakan komputer Model V yang sering error dan harus di-restart secara manual.
Pada masa itu, komputer Bell menggunakan sistem relay yang mudah mengalami kesalahan. Setiap kali terjadi error, mesin akan berhenti. Kemudian, operator harus datang untuk memperbaikinya. Sayangnya, Hamming sering bekerja di akhir pekan ketika tidak ada operator yang bertugas. Akibatnya, pekerjaannya sering tertunda.
Oleh karena itu, Hamming terdorong untuk mencari cara agar komputer bisa menemukan dan memperbaiki kesalahannya sendiri. Setelah meneliti selama beberapa tahun, akhirnya ia berhasil membuat kode koreksi error. Hasilnya dipublikasikan dalam paper berjudul “Error Detecting and Error Correcting Codes” pada tahun 1950.
Selain itu, Hamming juga memperkenalkan konsep jarak Hamming dan Hamming weight. Hingga sekarang, kedua konsep ini masih banyak digunakan dalam berbagai aplikasi coding dan keamanan data.
Prinsip Kerja Kode Hamming
Untuk memahami cara kerja kode Hamming, pertama-tama perlu dipahami beberapa konsep dasar. Secara umum, kode Hamming bekerja dengan menempatkan bit-bit parity pada posisi tertentu dalam blok data. Tujuannya adalah untuk menemukan dan memperbaiki error.
Posisi Bit Parity
Dalam kode Hamming, bit parity diletakkan pada posisi pangkat 2, yaitu posisi 1, 2, 4, 8, 16, dan seterusnya. Sementara itu, posisi lainnya diisi dengan bit data asli. Setiap bit parity bertugas memeriksa sejumlah bit tertentu berdasarkan pola biner dari posisinya.
Sebagai contoh, bit parity pada posisi 1 memeriksa semua bit yang posisinya memiliki angka 1 di digit terakhir binernya. Dengan kata lain, P1 memeriksa posisi 1, 3, 5, 7, 9, 11, dan seterusnya. Kemudian, bit parity pada posisi 2 memeriksa posisi 2, 3, 6, 7, 10, 11, dan seterusnya. Pola ini berlanjut untuk setiap bit parity.
Perhitungan Bit Parity
Nilai setiap bit parity ditentukan dari operasi XOR (exclusive OR) semua bit yang diperiksa. Jika menggunakan even parity, maka hasil XOR harus 0. Ini berarti jumlah bit bernilai 1 harus genap. Sebaliknya, jika menggunakan odd parity, hasil XOR harus 1.
Deteksi dan Koreksi Error
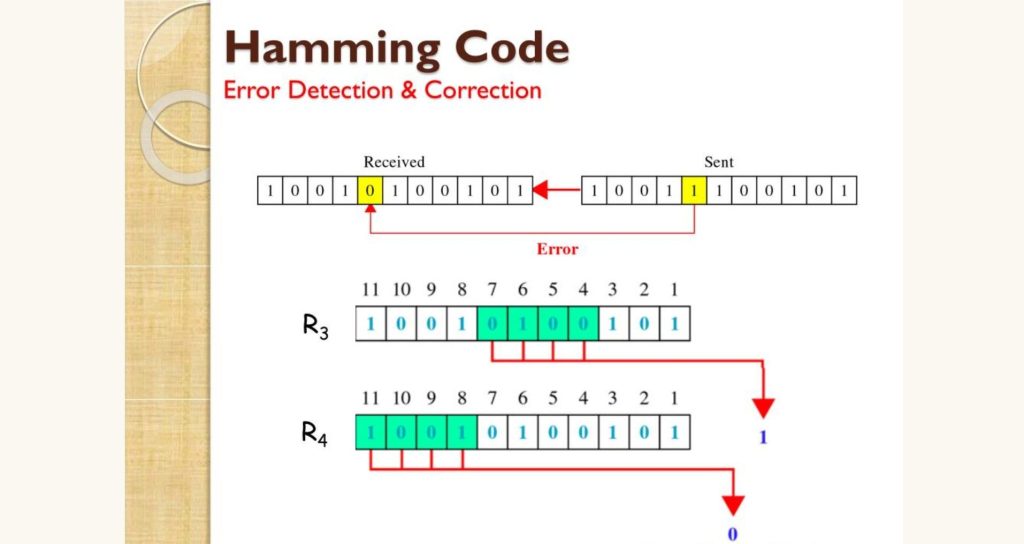
Ketika data diterima, penerima akan menghitung ulang nilai setiap bit parity. Lalu, hasilnya dibandingkan dengan bit parity yang diterima. Jika semua hitungan menghasilkan 0, berarti tidak ada error. Namun, jika ada bit parity yang tidak cocok, posisi-posisi tersebut dijumlahkan untuk menemukan lokasi bit yang salah.
Misalnya, jika P1 dan P4 menunjukkan ketidakcocokan, maka posisi error adalah 1 + 4 = 5. Selanjutnya, bit pada posisi 5 dibalik untuk memperbaiki kesalahan.
Rumus dan Perhitungan Kode Hamming
Untuk menerapkan kode Hamming, kita perlu tahu berapa banyak bit parity yang dibutuhkan. Berikut ini adalah rumus dan cara hitungnya.
Rumus Jumlah Bit Parity
Jika m adalah jumlah bit data dan r adalah jumlah bit parity, maka keduanya harus memenuhi rumus berikut:
2^r ≥ m + r + 1
Rumus ini memastikan bahwa bit parity cukup untuk menemukan semua kemungkinan posisi error. Nilai r terkecil yang memenuhi rumus tersebut adalah jumlah bit parity yang diperlukan.
Untuk memudahkan, berikut hubungan jumlah bit data dengan bit parity. Pertama, data 1 bit memerlukan 2 bit parity. Kedua, data 2-4 bit memerlukan 3 bit parity. Ketiga, data 5-11 bit memerlukan 4 bit parity. Terakhir, data 12-26 bit memerlukan 5 bit parity.
Notasi Kode Hamming
Kode Hamming biasanya ditulis dalam bentuk (n, k). Di sini, n adalah total panjang codeword dan k adalah jumlah bit data. Contoh paling umum adalah Hamming(7,4) yang berarti codeword 7 bit dengan 4 bit data dan 3 bit parity.
Contoh Perhitungan Kode Hamming
Agar lebih jelas, berikut ini contoh perhitungan kode Hamming secara bertahap.
Contoh Soal
Diberikan data 4 bit: 1011. Tentukan kode Hamming dengan even parity!
Langkah Penyelesaian
Langkah 1: Tentukan jumlah bit parity
Dengan m = 4 bit data, kita cari nilai r terkecil yang memenuhi 2^r ≥ 4 + r + 1. Untuk r = 3, maka 2^3 = 8 ≥ 8. Jadi, dibutuhkan 3 bit parity.
Langkah 2: Tentukan posisi bit
Total bit dalam codeword adalah 4 + 3 = 7 bit. Posisi bit parity adalah 1, 2, dan 4. Sementara itu, posisi bit data adalah 3, 5, 6, dan 7. Susunan awalnya adalah P1, P2, D1, P4, D2, D3, D4.
Langkah 3: Masukkan bit data
Dengan data 1011 yang dimasukkan ke posisi data, maka susunannya menjadi P1, P2, 1, P4, 0, 1, 1 pada posisi 1 sampai 7.
Langkah 4: Hitung nilai bit parity
Pertama, P1 memeriksa posisi 1, 3, 5, 7 dengan nilai ?, 1, 0, 1. Agar genap, maka P1 = 0. Kedua, P2 memeriksa posisi 2, 3, 6, 7 dengan nilai ?, 1, 1, 1. Agar genap, maka P2 = 1. Ketiga, P4 memeriksa posisi 4, 5, 6, 7 dengan nilai ?, 0, 1, 1. Agar genap, maka P4 = 0.
Langkah 5: Susun codeword final
Akhirnya, codeword lengkap menjadi 0, 1, 1, 0, 0, 1, 1 atau ditulis 0110011.
Verifikasi dengan Simulasi Error
Misalkan terjadi error pada posisi 5 sehingga data yang diterima adalah 0110111. Kemudian, penerima menghitung ulang dan menemukan hasil berikut.
Pertama, P1 bernilai 1 (error) karena posisi 1, 3, 5, 7 berisi 0, 1, 1, 1. Kedua, P2 bernilai 0 (OK) karena posisi 2, 3, 6, 7 berisi 1, 1, 1, 1. Ketiga, P4 bernilai 1 (error) karena posisi 4, 5, 6, 7 berisi 0, 1, 1, 1.
Dengan demikian, posisi error adalah P1 + P4 = 1 + 4 = 5. Selanjutnya, bit pada posisi 5 dibalik dari 1 menjadi 0. Hasilnya, data terkoreksi menjadi 0110011.
Aplikasi Kode Hamming dalam Kehidupan Nyata
Kode Hamming punya banyak penerapan dalam dunia teknologi. Berikut ini beberapa contoh penggunaannya.
Memori Komputer (ECC RAM)
Salah satu penerapan paling umum adalah pada ECC RAM yang digunakan di server. ECC RAM menggunakan prinsip kode Hamming untuk menemukan dan memperbaiki single-bit error secara otomatis. Selain itu, sistem ini juga bisa menemukan double-bit error. Oleh karena itu, ECC RAM sangat penting untuk server yang butuh keandalan tinggi.
Penyimpanan Data
Hard disk dan SSD modern menggunakan berbagai teknik koreksi error yang didasarkan pada prinsip kode Hamming. Dengan demikian, data yang tersimpan tetap bisa dibaca dengan benar meskipun ada kerusakan kecil pada media penyimpanan.
Telekomunikasi
Dalam sistem satelit dan jaringan wireless, kode Hamming digunakan untuk menjaga keutuhan data. Hasilnya, komunikasi tetap lancar bahkan dalam kondisi sinyal yang kurang baik.
QR Code dan Barcode
Sistem barcode dan QR code juga menggunakan teknik koreksi error yang berasal dari konsep kode Hamming. Itulah mengapa QR code masih bisa terbaca meskipun sebagian areanya rusak atau tertutup.
Kelebihan dan Keterbatasan Kode Hamming
Seperti teknologi lainnya, kode Hamming punya kelebihan dan keterbatasan yang perlu dipahami.
Kelebihan
Kode Hamming memiliki beberapa keunggulan. Pertama, kemampuannya untuk tidak hanya menemukan tetapi juga memperbaiki error single-bit secara otomatis. Kedua, overhead yang cukup rendah dibanding metode lain yang lebih rumit. Ketiga, cara kerjanya sederhana karena hanya menggunakan operasi logika dasar seperti XOR. Keempat, proses encoding dan decoding yang cepat karena hitungannya ringan.
Keterbatasan
Di sisi lain, kode Hamming standar punya beberapa batasan. Metode ini hanya bisa memperbaiki satu bit error per blok data. Jika terjadi dua atau lebih bit error, sistem mungkin gagal menemukan atau bahkan salah memperbaiki. Untuk mengatasi hal ini, dikembangkan versi lain seperti SECDED yang menambahkan satu bit parity ekstra.
Pengembangan Lanjutan Kode Hamming
Konsep dasar kode Hamming telah dikembangkan lebih lanjut untuk memenuhi kebutuhan aplikasi modern.
Extended Hamming Code
Extended Hamming Code menambahkan satu bit parity di posisi 0 untuk membentuk kode SECDED. Dengan penambahan ini, sistem bisa memperbaiki semua single-bit error dan menemukan semua double-bit error. Hasilnya, perlindungan data menjadi lebih lengkap.
Reed-Solomon Code
Reed-Solomon Code adalah pengembangan dari konsep Hamming yang bisa memperbaiki multiple-byte error. Metode ini banyak digunakan pada CD, DVD, Blu-ray, serta sistem komunikasi luar angkasa NASA.
LDPC dan Turbo Code
LDPC Code dan Turbo Code adalah pengembangan modern dengan performa sangat tinggi. Saat ini, kode-kode ini digunakan pada standar terbaru seperti 5G, WiFi 6, dan DVB-S2.
Tips Belajar Kode Hamming untuk Mahasiswa
Bagi mahasiswa yang sedang belajar materi ini, berikut beberapa tips yang bisa membantu.
Pertama, pahami dulu konsep dasar operasi XOR karena ini adalah fondasi dari semua hitungan kode Hamming. Kedua, latih konversi bilangan desimal ke biner dan sebaliknya hingga lancar. Ketiga, gunakan tabel atau gambar untuk melihat posisi bit dan cakupan setiap bit parity. Keempat, kerjakan banyak contoh soal dengan variasi jumlah bit data yang berbeda. Kelima, coba buat program sederhana untuk menghitung kode Hamming agar lebih paham logikanya.
Penutup
Singkatnya, kode Hamming adalah salah satu penemuan penting dalam bidang teori informasi yang hingga kini masih banyak digunakan. Pemahaman yang baik tentang konsep ini tidak hanya penting untuk kuliah, tetapi juga menjadi dasar untuk memahami teknik koreksi error yang lebih canggih.
Bagi mahasiswa teknik informatika, menguasai kode Hamming akan membantu memahami bagaimana sistem komputer modern menjaga keutuhan data. Dengan terus berlatih dan mengerjakan contoh soal, konsep yang awalnya terasa sulit akan menjadi lebih mudah dipahami.
Semoga artikel ini bermanfaat untuk proses belajar. Untuk materi kuliah lainnya seputar teknik informatika dan sistem informasi, kunjungi terus studyinca.ac.id sebagai sumber referensi belajar yang terpercaya.
Baca juga konten dengan artikel terkait tentang: Pengetahuan
Baca juga artikel lainnya: Senam Lantai dasar keterampilan tubuh dalam pendidikan jasmani