JAKARTA, studyinca.ac.id – Konsep bilangan bulat sudah dikenal sejak zaman kuno. Bangsa Mesir dan Babilonia telah menggunakan bilangan positif untuk menghitung hasil panen, perdagangan, dan pajak. Namun, bilangan negatif baru diterima jauh lebih kemudian.
Bangsa India pada abad ke-7 mulai memperkenalkan ide bilangan negatif dalam perhitungan utang dan rugi. Konsep ini kemudian masuk ke dunia Arab, diterjemahkan, dan menyebar ke Eropa pada abad pertengahan. Pada awalnya, bilangan negatif dianggap “tidak nyata” atau “tidak masuk akal”. Namun, seiring berkembangnya ilmu matematika, terutama dalam aljabar dan persamaan linear, bilangan negatif diakui sebagai bagian penting dalam himpunan bilanganbulat.
Perbandingan Bilangan Bulat dengan Himpunan Bilangan Lain
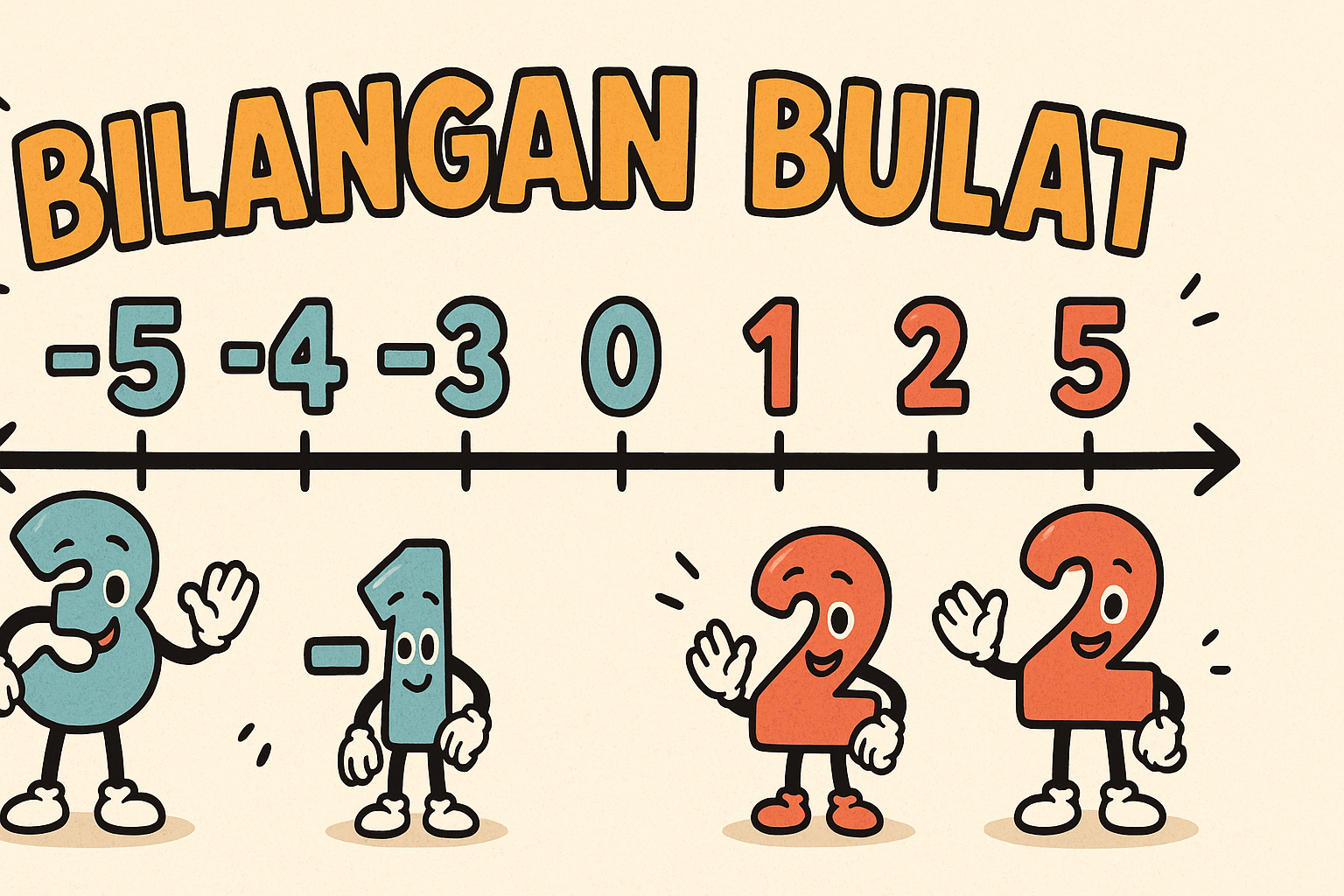
Untuk memahami posisi bilangan bulat, perlu dibandingkan dengan himpunan bilangan lainnya:
-
Bilangan Asli (N): 1, 2, 3, 4, …
→ Tidak termasuk nol dan bilangan negatif. -
Bilangan Cacah: 0, 1, 2, 3, …
→ Sama seperti bilangan asli tetapi termasuk nol. -
Bilangan Bulat (Z): …, -3, -2, -1, 0, 1, 2, 3, …
→ Mencakup positif, negatif, dan nol. -
Bilangan Rasional (Q): mencakup pecahan, seperti ½ atau -3/4.
-
Bilangan Real (R): mencakup semua bilangan rasional dan irasional.
Posisi bilanganbulat bisa dikatakan sebagai jembatan antara bilangan cacah dan bilangan rasional.
Representasi BilanganBulat di Garis Bilangan
Salah satu cara visual paling mudah memahami bilangan bulat adalah dengan garis bilangan.
-
Angka 0 terletak di tengah.
-
Bilangan positif berada di kanan 0.
-
Bilangan negatif berada di kiri 0.
Dengan garis bilangan, operasi penjumlahan dan pengurangan dapat divisualisasikan. Misalnya:
-
3 + (-2) berarti bergerak 3 langkah ke kanan, lalu 2 langkah ke kiri → hasilnya 1.
-
-4 + 6 berarti bergerak 4 langkah ke kiri, lalu 6 langkah ke kanan → hasilnya 2.
Bilangan Bulat dalam Kehidupan Modern
-
Keuangan Digital
Dalam sistem perbankan, bilangan bulat dipakai untuk mencatat saldo. Kredit ditulis sebagai bilangan positif, debit atau utang ditulis sebagai bilangan negatif. -
Pemrograman Komputer
Dalam dunia coding, bilanganbulat disebut integer. Hampir semua bahasa pemrograman seperti Java, Python, atau C menggunakan bilanganbulat untuk menghitung data diskrit, menghitung loop, atau memanipulasi array. -
Fisika
Dalam mekanika, arah gerakan benda bisa dinyatakan dengan bilanganbulat. Positif untuk arah maju, negatif untuk arah berlawanan. -
Ilmu Sosial
Statistik jumlah penduduk, tingkat pengangguran, dan data sensus umumnya dihitung dalam bilanganbulat.
Contoh Soal Bilangan Bulat
-
Penjumlahan
Hitung: (-7) + 12 = ?
→ Hasilnya = 5. -
Pengurangan
Hitung: 15 – (-4) = ?
→ Sama dengan 15 + 4 = 19. -
Perkalian
Hitung: (-8) × (-6) = ?
→ Dua negatif menghasilkan positif, hasil = 48. -
Pembagian
Hitung: (-24) ÷ 6 = ?
→ Hasilnya = -4. -
Soal Cerita
Suhu udara di kota A pada pagi hari -3°C. Siang hari suhu naik 8°C. Berapakah suhu siang hari?
→ -3 + 8 = 5°C.
Pentingnya Bilangan Bulat dalam Pendidikan
Bilangan bulat diajarkan sejak tingkat sekolah dasar. Tujuannya bukan hanya agar siswa bisa menghitung, tetapi juga melatih pola pikir logis.
-
Sekolah Dasar: Fokus pada konsep positif, negatif, dan nol.
-
Sekolah Menengah: Penggunaan bilanganbulat dalam persamaan linear, aljabar, dan grafik.
-
Perguruan Tinggi: Digunakan dalam teori bilangan, kriptografi, hingga algoritma komputer.
Kesalahan umum siswa adalah saat mengoperasikan tanda negatif. Oleh karena itu, penggunaan garis bilangan dan soal cerita sangat membantu memperkuat pemahaman.
Kesadaran Numerik di Masyarakat
Kemampuan memahami bilangan bulat ternyata berhubungan langsung dengan literasi numerik masyarakat. Misalnya, saat membaca laporan ekonomi, cuaca, atau statistik, bilanganbulat selalu muncul.
-
Perubahan indeks saham: +20 poin atau -15 poin.
-
Suhu harian: 30°C siang hari, -2°C malam hari.
-
Data sensus: Pertumbuhan penduduk +1,2 juta, penurunan migrasi -500 ribu.
Tanpa pemahaman bilanganbulat, masyarakat bisa salah menafsirkan data penting yang berdampak pada kehidupan sehari-hari.
Tantangan dan Kesalahan Umum dalam Memahami BilanganBulat
-
Negatif dengan Negatif
Banyak siswa bingung mengapa (-4) – (-2) = -2. Padahal, konsepnya adalah mengubah pengurangan menjadi penjumlahan lawan. -
Pembagian Nol
Tidak ada bilangan bulat yang bisa dibagi dengan nol. Konsep ini penting agar tidak terjadi salah kaprah dalam matematika. -
Pemakaian dalam Kehidupan Nyata
Kadang orang sulit membayangkan bilangan negatif. Guru biasanya memberi contoh suhu, kedalaman laut, atau rugi laba agar lebih mudah dipahami.
Rencana Perluasan Artikel
-
Pendahuluan yang Lebih Panjang
-
Menambahkan sejarah singkat tentang bilangan bulat dari peradaban kuno hingga modern.
-
Penjelasan mengapa bilangan bulat penting dalam pendidikan matematika.
-
-
Klasifikasi dengan Penjelasan Detail
-
Tambahkan ilustrasi praktis: bilangan positif untuk untung, bilangan negatif untuk rugi, dan nol sebagai titik netral.
-
Perbandingan bilangan bulat dengan bilangan cacah, asli, dan rasional.
-
-
Operasi Bilangan Bulat dengan Contoh Lebih Banyak
-
Setiap operasi (penjumlahan, pengurangan, perkalian, pembagian) ditambahkan contoh soal cerita.
-
Visualisasi dengan garis bilangan untuk memperkuat pemahaman.
-
-
Aplikasi dalam Kehidupan Sehari-hari
-
Lebih rinci di bidang keuangan, suhu, ketinggian, skor olahraga, hingga teknologi komputer.
-
Tambahkan contoh nyata seperti saldo rekening bank, skor game online, hingga data populasi.
-
-
Peranan dalam Matematika Lanjut
-
Pembahasan lebih dalam pada teori bilangan, aljabar, kriptografi, dan pemrograman komputer.
-
-
Latihan Soal dan Pembahasan
-
Tambahkan 5–7 contoh soal beserta langkah-langkah jawaban.
-
-
Kesimpulan yang Lebih Kuat
-
Ringkas manfaat bilangan bulat sebagai fondasi berpikir logis dan aplikatif dalam kehidupan.
-
Kesimpulan
Bilangan bulat bukan hanya bagian dasar matematika, melainkan juga alat penting dalam kehidupan modern. Dari sejarahnya yang panjang hingga penerapannya dalam teknologi, ekonomi, hingga pendidikan, bilanganbulat tetap relevan.
Dengan memahami bilanganbulat, seseorang tidak hanya bisa menghitung, tetapi juga mengembangkan pola pikir logis, kritis, dan terstruktur. Hal ini membuktikan bahwa matematika, meski sering dianggap rumit, sesungguhnya adalah bahasa universal yang membantu manusia memahami dunia.
Baca juga konten dengan artikel terkait tentang: Pengetahuan
Baca juga artikel lainnya: GitHub Classroom dan Transformasi Pembelajaran Digital

