JAKARTA, studyinca.ac.id – Di sebuah kelas matematika sekolah dasar, seorang guru mengangkat kue bulat yang dibagi menjadi delapan bagian sama besar. Seorang reporter pendidikan yang hadir tersenyum sambil berkata: “Inilah cara sederhana menjelaskan bilangan pecahan. Satu potong dari delapan adalah 1/8. Semakin nyata, semakin mudah dipahami.”
Pemandangan itu memperlihatkan bahwa matematika tidak selalu harus berupa angka di papan tulis. Dengan benda nyata, konsep pecahan menjadi hidup. Anak-anak dapat langsung melihat bagaimana keseluruhan dibagi, bagaimana satu bagian merepresentasikan sebuah pecahan, dan bagaimana pecahan itu bisa digabungkan kembali menjadi satu utuh.
Bilangan pecahan sering menjadi momok bagi sebagian siswa, bahkan hingga ke jenjang menengah. Padahal, pecahan justru sangat dekat dengan keseharian kita. Mulai dari resep masakan, pembagian waktu belajar, hingga diskon belanja di pusat perbelanjaan, semuanya melibatkan pecahan. Dengan kata lain, pecahan adalah bahasa universal yang membantu kita memahami proporsi dalam kehidupan nyata.
Apa Itu Bilangan Pecahan
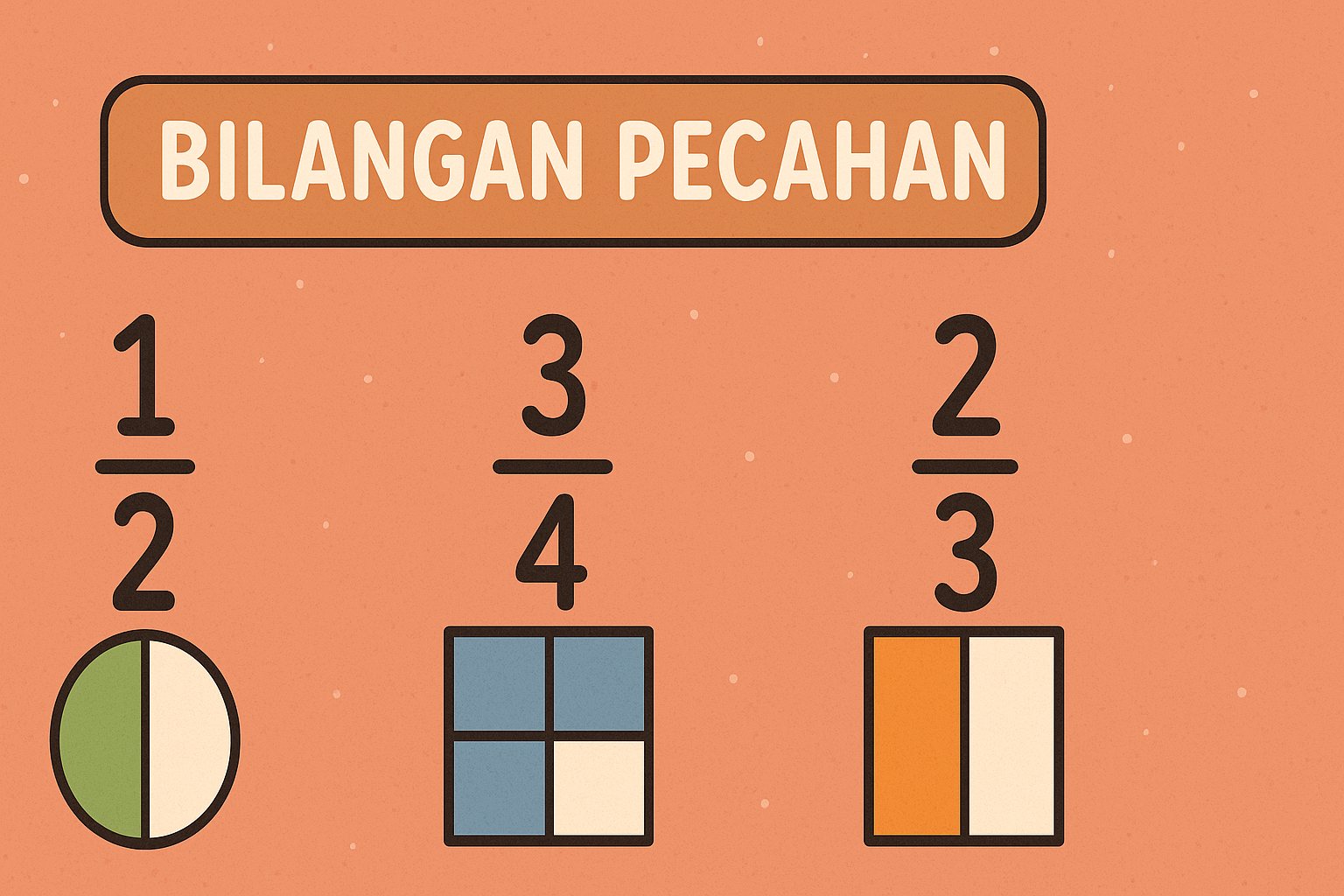
Bilangan pecahan adalah bilangan yang menyatakan bagian dari keseluruhan. Bentuk umum pecahan ditulis a/b, di mana:
-
a disebut pembilang, yang menunjukkan bagian yang diambil,
-
b disebut penyebut, yang menunjukkan jumlah keseluruhan yang sama besar.
Contoh sederhana: 3/4 artinya tiga bagian dari empat bagian yang sama besar. Jika sebuah pizza dibagi menjadi 4 potong sama besar dan seseorang memakan 3 potong, maka ia telah memakan ¾ pizza.
Pecahan tidak hanya terbatas pada makanan atau benda fisik. Ia juga hadir dalam pembagian jarak, pengukuran waktu, hingga konsep abstrak seperti peluang dalam statistika.
Jenis-Jenis Pecahan
Dalam pembelajaran, pecahan dibagi ke dalam beberapa jenis utama:
-
Pecahan Biasa
Ditulis dalam bentuk a/b. Contoh: 2/5 artinya dua bagian dari lima bagian. -
Pecahan Campuran
Gabungan bilangan bulat dengan pecahan, contohnya 2 ½. Artinya dua utuh ditambah setengah. -
Pecahan Senilai
Pecahan yang nilainya sama meski bentuknya berbeda. Misalnya 1/2 = 2/4 = 4/8. Konsep ini penting untuk menyederhanakan atau memperluas pecahan. -
Pecahan Desimal
Pecahan dengan penyebut 10, 100, atau 1000, ditulis dengan tanda koma. Contoh: 0,25 adalah 25/100. -
Pecahan Persen
Pecahan dengan penyebut 100, ditulis dengan tanda %. Contoh: 75% = 75/100 = 3/4.
Memahami jenis-jenis pecahan ini membantu siswa melihat hubungan antarformat bilangan. Misalnya, menyadari bahwa 0,5 = 50% = 1/2 membuat siswa lebih luwes dalam berhitung.
Operasi Hitung Bilangan Pecahan
Sama seperti bilangan bulat, Bilangan Pecahan juga dapat dioperasikan dengan aturan tertentu.
-
Penjumlahan dan Pengurangan
-
Jika penyebut sama: jumlahkan atau kurangi pembilang.
Contoh: 2/7 + 3/7 = 5/7. -
Jika penyebut berbeda: samakan penyebut terlebih dahulu.
Contoh: 1/2 + 1/3 = 3/6 + 2/6 = 5/6.
-
-
Perkalian Pecahan
Cukup kalikan pembilang dengan pembilang, penyebut dengan penyebut.
Contoh: 2/3 × 3/5 = 6/15 = 2/5. -
Pembagian Pecahan
Balik pecahan kedua (resiprokalnya), lalu lakukan perkalian.
Contoh: 2/3 ÷ 4/5 = 2/3 × 5/4 = 10/12 = 5/6.
Latihan operasi pecahan sering menantang, terutama saat penyebut berbeda. Namun dengan latihan bertahap, siswa akan terbiasa.
Aplikasi Pecahan dalam Kehidupan Sehari-hari
Konsep Bilangan Pecahan hidup di sekitar kita:
-
Memasak: resep sering menggunakan pecahan, misalnya ½ sendok teh garam atau ¾ cangkir gula. Tanpa pemahaman pecahan, resep akan gagal.
-
Waktu: ¼ jam = 15 menit. Banyak aktivitas terukur dalam pecahan waktu.
-
Keuangan: diskon 25% berarti potongan 1/4 harga. Dalam investasi, pecahan digunakan untuk menghitung bunga atau persentase keuntungan.
-
Olahraga: statistik pemain basket, misalnya sukses 7/10 tembakan, berarti 70%. Pecahan membantu mengubah data menjadi informasi mudah dipahami.
-
Arsitektur dan teknik: ukuran bahan bangunan atau desain sering membutuhkan pecahan, misalnya ½ meter atau 3/8 inci.
Kesulitan Umum dan Cara Mengatasinya Bilangan Pecahan
Banyak siswa kesulitan karena tidak terbiasa membayangkan bagian dari keseluruhan. Ada beberapa strategi untuk mengatasinya:
-
Gunakan benda nyata
Kue, pizza, kertas lipat, atau balok warna-warni bisa jadi alat bantu visual yang efektif. -
Latih dengan soal kontekstual
Soal sehari-hari, seperti pembagian buah atau hitungan waktu belajar, membuat pecahan terasa relevan. -
Gunakan diagram visual
Diagram lingkaran, diagram batang, atau persegi berpetak membantu siswa menghubungkan pecahan dengan gambar nyata. -
Hubungkan dengan desimal dan persen
Dengan membiasakan siswa bahwa 0,5 = 50% = 1/2, konsep pecahan menjadi lebih fleksibel.
Pecahan dalam Perspektif Lebih Luas
Bilangan Pecahan tidak hanya hadir di sekolah dasar. Dalammatematika lanjutan, pecahan berkembang menjadi rasio, proporsi, bahkan pecahan aljabar yang dipakai di fisika dan ekonomi. Dalam statistika, pecahan menjadi pondasi peluang. Dalam ilmu sosial, pecahan digunakan untuk membaca persentase data survei.
Dengan kata lain, pemahaman pecahan adalah jembatan menuju pemahaman ilmu lain. Seorang anak yang memahami pecahan dengan baik akan lebih siap menghadapi materi matematika tingkat lanjut.
Refleksi Penutup: Belajar dari Bilangan Pecahan
Reporter pendidikan menutup siaran dengan kalimat: “Setiap bagian kecil menyusun keseluruhan. Pecahan mengajarkan kita menghargai proporsi. Dalam hidup, seringkali 1/4 langkah berani bisa mengubah 3/4 jalan berikutnya.”
Bilangan pecahan bukan hanya konsep angka. Ia adalah refleksi cara manusia memahami keterbatasan, keadilan, dan pembagian dalam kehidupan nyata. Dari kue di kelas hingga laporan keuangan perusahaan, pecahan mengajarkan kita satu hal: bahwa bagian kecil memiliki arti besar jika ditempatkan dengan benar.
Baca juga konten dengan artikel terkait tentang: Pengetahuan
Baca juga artikel lainnya: Bilangan Negatif: Konsep, Sejarah, dan Pemahaman

