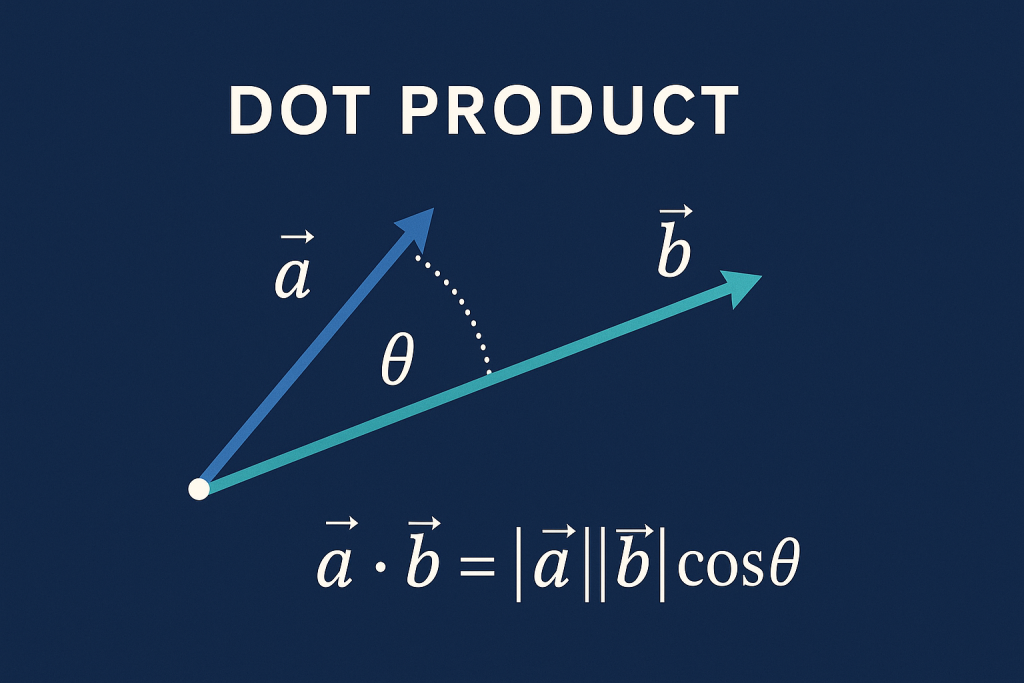
JAKARTA, studyinca.ac.id – Dalam dunia matematika dan fisika, operasi vektor merupakan salah satu konsep fundamental yang memiliki aplikasi luas. Sebagai contoh, mulai dari perhitungan gaya dalam mekanika hingga pemrosesan data dalam machine learning. Namun demikian, tidak semua mahasiswa memahami berbagai jenis operasi vektor secara mendalam. Di sinilah pentingnya mempelajari dot product atau perkalian titik sebagai salah satu operasi vektor yang paling sering digunakan. Lebih dari sekadar perkalian biasa, dot product memiliki karakteristik unik yang menghasilkan nilai skalar dari dua vektor. Dengan demikian, pemahaman konsep ini menjadi dasar penting untuk mempelajari topik-topik lanjutan dalam aljabar linear dan kalkulus vektor.
Relevansi Dot Product dalam Pendidikan Tinggi
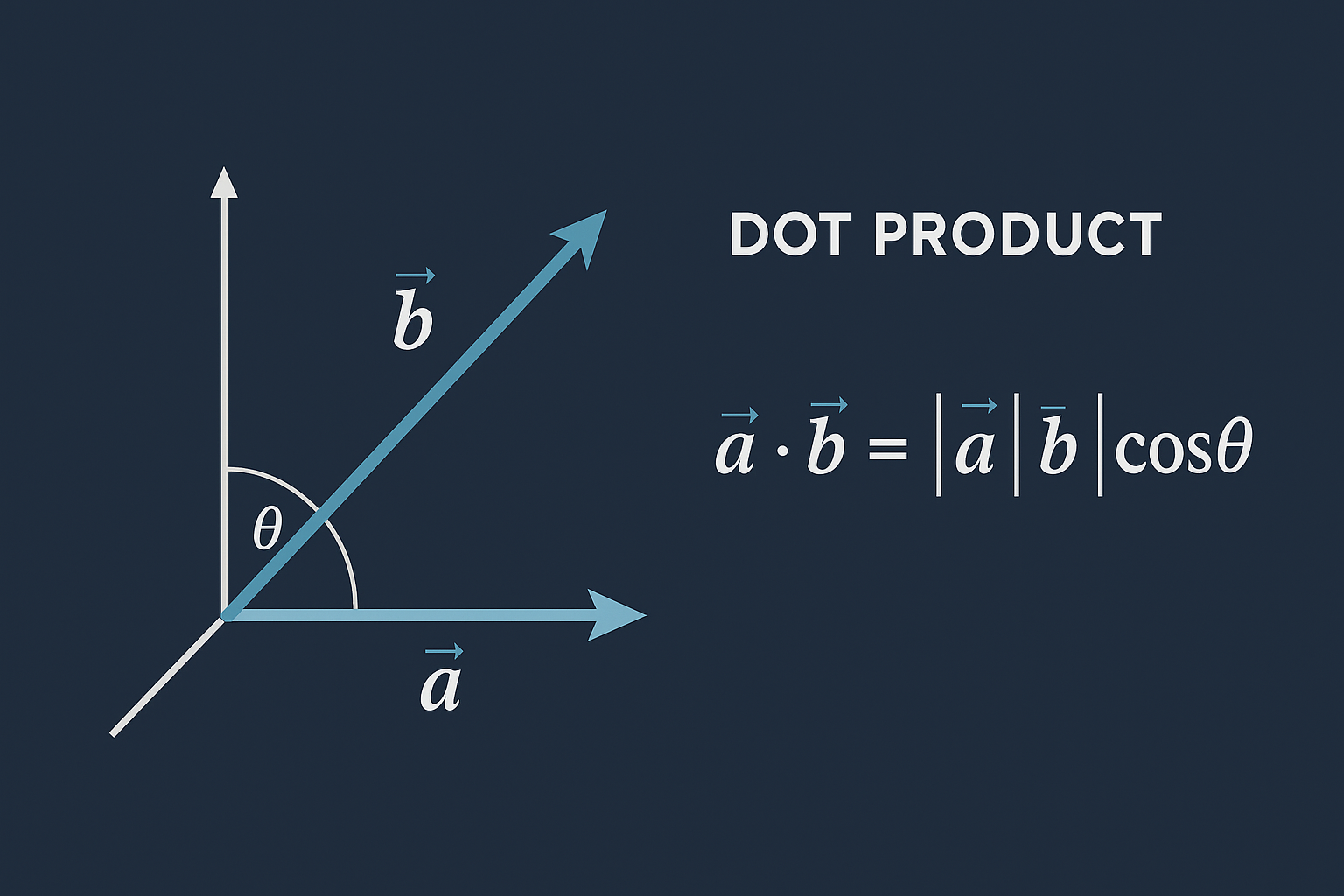
Dalam konteks akademis, dot product menjadi salah satu materi wajib yang harus dikuasai oleh mahasiswa STEM (Science, Technology, Engineering, and Mathematics). Lebih lanjut, kemampuan menghitung dan menerapkan dot product tidak hanya berguna untuk mengerjakan soal ujian, tetapi juga untuk memahami fenomena fisika dan teknik yang kompleks. Pada kenyataannya, banyak algoritma komputasi modern yang memanfaatkan operasi dot product dalam prosesnya. Oleh karena itu, memahami konsep, rumus, dan aplikasi dot product menjadi sangat penting bagi siapa saja yang ingin mendalami bidang sains dan teknologi secara serius.
Pengertian Dot Product secara Komprehensif
Definisi Matematis Dot Product
Dot product atau perkalian titik adalah operasi matematika yang mengambil dua vektor dengan dimensi yang sama dan menghasilkan sebuah bilangan skalar tunggal. Secara lebih spesifik, operasi ini menghitung hasil kali komponen-komponen yang bersesuaian dari kedua vektor, kemudian menjumlahkan semua hasil kali tersebut. Dengan kata lain, dot product mengubah dua vektor input menjadi satu nilai numerik output. Menariknya, hasil operasi ini bersifat komutatif, artinya urutan vektor yang dikalikan tidak mempengaruhi hasilnya.
Notasi dan Simbol Dot Product
Dalam penulisan matematis, dot product biasanya dilambangkan dengan simbol titik (·) di antara kedua vektor. Sebagai contoh, dot product dari vektor a dan vektor b ditulis sebagai a · b. Sementara itu, dalam notasi matriks, operasi ini sering ditulis sebagai aᵀb, di mana superskrip T menunjukkan transpose. Pada dasarnya, kedua notasi ini merujuk pada operasi yang sama namun dengan representasi yang berbeda. Lebih lanjut, konsistensi penggunaan notasi sangat penting untuk menghindari kebingungan dalam penulisan matematika.
Karakteristik utama dot product:
- Pertama, menghasilkan nilai skalar bukan vektor
- Kedua, memerlukan dua vektor dengan dimensi sama
- Ketiga, bersifat komutatif dan distributif
- Keempat, nilai nol menunjukkan kedua vektor tegak lurus
- Kelima, nilai positif menunjukkan sudut lancip antara vektor
- Keenam, nilai negatif menunjukkan sudut tumpul antara vektor
- Ketujuh, digunakan untuk menghitung proyeksi vektor
- Terakhir, fundamental dalam banyak aplikasi fisika dan teknik
Perbedaan Dot Product dengan Cross Product
Perlu dipahami bahwa dot product berbeda dengan cross product atau perkalian silang. Pertama dan terutama, dot product menghasilkan skalar sedangkan cross product menghasilkan vektor baru. Kedua, dot product dapat diterapkan pada vektor dengan dimensi berapa pun, sementara cross product umumnya didefinisikan untuk vektor tiga dimensi. Dengan demikian, pemilihan operasi yang tepat tergantung pada hasil yang diinginkan dan konteks permasalahan. Selain itu, kedua operasi ini memiliki interpretasi geometris yang berbeda dan aplikasi yang spesifik.
Rumus Dot Product dalam Berbagai Bentuk
Formula Aljabar untuk Vektor Dimensi-n
Untuk dua vektor a = (a₁, a₂, a₃, …, aₙ) dan b = (b₁, b₂, b₃, …, bₙ), dot product didefinisikan secara aljabar sebagai jumlah hasil kali komponen-komponen yang bersesuaian. Secara matematis, rumus ini ditulis sebagai a · b = a₁b₁ + a₂b₂ + a₃b₃ + … + aₙbₙ. Menariknya, formula sederhana ini berlaku untuk vektor dengan dimensi berapa pun, mulai dari dua dimensi hingga dimensi tak hingga dalam ruang Hilbert. Lebih lanjut, kesederhanaan rumus ini membuatnya mudah diimplementasikan dalam program komputer dan kalkulator.
Rumus Geometris dengan Sudut
Alternatif lain, dot product juga dapat dinyatakan dalam bentuk geometris yang melibatkan besar vektor dan sudut di antara keduanya. Secara spesifik, a · b = |a| |b| cos θ, di mana |a| dan |b| adalah magnitudo kedua vektor, sedangkan θ adalah sudut antara mereka. Pada kenyataannya, formula geometris ini sangat berguna untuk menghitung sudut antara dua vektor atau menentukan proyeksi satu vektor pada vektor lainnya. Dengan demikian, kedua bentuk rumus ini saling melengkapi dan dapat digunakan bergantian sesuai kebutuhan.
Bentuk-bentuk rumus dot product:
- Pertama, bentuk aljabar untuk komputasi langsung
- Kedua, bentuk geometris untuk interpretasi sudut
- Ketiga, bentuk matriks untuk operasi linear
- Keempat, bentuk integral untuk fungsi kontinu
- Terakhir, bentuk diskrit untuk data digital
Contoh Perhitungan Sederhana Dot Product
Mari kita ambil contoh konkret untuk memperjelas pemahaman. Misalkan vektor a = (3, 4) dan vektor b = (2, 1) dalam ruang dua dimensi. Dengan demikian, dot product a · b = (3)(2) + (4)(1) = 6 + 4 = 10. Hasil ini adalah bilangan skalar tunggal. Selanjutnya, untuk memverifikasi dengan rumus geometris, kita perlu menghitung magnitudo dan sudut. Lebih lanjut, |a| = √(3² + 4²) = 5 dan |b| = √(2² + 1²) = √5. Oleh karena itu, cos θ = 10/(5√5) = 2/√5, yang memberikan θ ≈ 26.57°.
Sifat-Sifat Dot Product yang Fundamental
Sifat Komutatif dan Distributif
Dot product memiliki beberapa sifat aljabar yang sangat penting untuk manipulasi matematika. Pertama, sifat komutatif menyatakan bahwa a · b = b · a, artinya urutan perkalian tidak mempengaruhi hasil. Kedua, sifat distributif terhadap penjumlahan vektor berlaku, yaitu a · (b + c) = a · b + a · c. Menariknya, sifat-sifat ini memungkinkan kita untuk menyederhanakan ekspresi aljabar yang kompleks. Dengan demikian, pemahaman sifat-sifat ini sangat membantu dalam pembuktian teorema dan penyelesaian masalah.
Sifat-sifat matematis penting:
- Pertama, komutatif dalam urutan operasi
- Kedua, distributif terhadap penjumlahan vektor
- Ketiga, asosiatif terhadap perkalian skalar
- Keempat, menghasilkan nol untuk vektor ortogonal
- Kelima, positif definitif untuk vektor dengan dirinya sendiri
- Terakhir, linear pada setiap argumen vektor
Sifat Ortogonalitas Vektor Dot Product
Salah satu aplikasi penting dot product adalah menentukan ortogonalitas atau ketegarlurusan dua vektor. Secara matematis, dua vektor a dan b dikatakan ortogonal jika dan hanya jika a · b = 0. Pada kenyataannya, kondisi ini ekuivalen dengan mengatakan bahwa sudut antara kedua vektor adalah 90 derajat. Lebih lanjut, konsep ortogonalitas ini fundamental dalam banyak aplikasi, seperti dekomposisi vektor dan konstruksi basis ortogonal. Dengan demikian, dot product menjadi alat yang sangat efektif untuk memeriksa ketegarlurusan dalam ruang vektor.
Sifat Homogenitas dan Linearitas
Dot product juga memiliki sifat homogenitas terhadap perkalian skalar. Artinya, (ca) · b = c(a · b), di mana c adalah konstanta skalar. Selain itu, operasi ini bersifat linear pada setiap argumennya, yang berarti a · (b + c) = a · b + a · c dan (a + b) · c = a · c + b · c. Pada dasarnya, sifat-sifat ini menjadikan dotproduct sebagai contoh dari fungsi bilinear. Lebih lanjut, linearitas ini sangat penting dalam teori ruang vektor dan operator linear.
Interpretasi Geometris Dot Product
Proyeksi Vektor pada Vektor Lain
Salah satu interpretasi geometris paling penting dari dotproduct adalah hubungannya dengan proyeksi vektor. Secara khusus, proyeksi ortogonal vektor a pada vektor b dapat dihitung menggunakan formula projb(a) = [(a · b) / |b|²] b. Menariknya, panjang proyeksi ini sama dengan |a| cos θ, yang merupakan komponen vektor a dalam arah b. Dengan demikian, dotproduct memberikan cara efisien untuk mendekomposisi vektor menjadi komponen paralel dan tegak lurus. Lebih lanjut, konsep proyeksi ini sangat berguna dalam berbagai aplikasi fisika dan rekayasa.
Mengukur Kemiripan dan Sudut Antar Vektor
Dalam konteks geometris, dot product dapat digunakan untuk mengukur seberapa “mirip” atau “sejalan” dua vektor. Secara kuantitatif, nilai dotproduct yang besar (positif) menunjukkan bahwa kedua vektor menunjuk ke arah yang hampir sama. Sebaliknya, nilai negatif besar menunjukkan arah yang berlawanan. Pada kenyataannya, nilai nol menunjukkan kedua vektor saling tegak lurus atau tidak memiliki komponen dalam arah yang sama. Dengan demikian, dotproduct menjadi ukuran alami untuk kemiripan arah dalam ruang vektor.
Interpretasi nilai dot product:
- Pertama, positif besar berarti sudut lancip kecil
- Kedua, nol menunjukkan vektor tegak lurus sempurna
- Ketiga, negatif besar berarti sudut tumpul mendekati 180°
- Keempat, magnitudo menunjukkan tingkat kesejajaran
- Terakhir, dapat dinormalisasi untuk mendapat cosine similarity
Menghitung Sudut Antara Dua Vektor
Dengan memanfaatkan rumus geometris, kita dapat menghitung sudut antara dua vektor dengan mudah. Secara spesifik, θ = arccos[(a · b) / (|a| |b|)]. Formula ini sangat praktis karena hanya memerlukan operasi dot product dan perhitungan magnitudo. Lebih lanjut, metode ini berlaku untuk vektor dalam dimensi berapa pun, tidak hanya dua atau tiga dimensi. Oleh karena itu, dotproduct menjadi alat fundamental dalam geometri vektor dan trigonometri lanjutan.
Aplikasi Dot Product dalam Fisika
Perhitungan Kerja dalam Mekanika
Dalam fisika mekanika, konsep kerja (work) didefinisikan secara matematis menggunakan dot product. Secara spesifik, kerja yang dilakukan oleh gaya F yang menyebabkan perpindahan d dihitung sebagai W = F · d. Menariknya, formula ini secara otomatis memperhitungkan fakta bahwa hanya komponen gaya dalam arah perpindahan yang melakukan kerja. Dengan demikian, jika gaya tegak lurus perpindahan, tidak ada kerja yang dilakukan meskipun ada gaya dan perpindahan. Lebih lanjut, pemahaman ini fundamental dalam termodinamika dan konservasi energi.
Analisis Komponen Gaya Dot Product
Dot product juga sangat berguna untuk menganalisis komponen gaya dalam berbagai arah. Sebagai contoh, untuk mengetahui berapa besar gaya yang bekerja dalam arah tertentu, kita dapat menghitung dotproduct antara vektor gaya dan vektor satuan dalam arah yang diminati. Pada kenyataannya, teknik ini sering digunakan dalam mekanika untuk menganalisis sistem gaya yang kompleks. Selain itu, metode ini juga memudahkan perhitungan dalam sistem koordinat yang berbeda.
Aplikasi dalam mekanika:
- Pertama, menghitung kerja mekanis total
- Kedua, menentukan komponen gaya efektif
- Ketiga, menganalisis energi kinetik sistem
- Keempat, menghitung torsi dan momen gaya
- Kelima, mengevaluasi daya mekanis
- Terakhir, menganalisis getaran dan osilasi
Listrik dan Medan Vektor
Dalam elektromagnetisme, dot product digunakan secara ekstensif untuk menghitung fluks listrik dan magnetik. Secara khusus, fluks medan listrik E melalui permukaan dengan vektor normal A dihitung sebagai Φ = E · A. Menariknya, konsep fluks ini fundamental dalam hukum Gauss dan persamaan Maxwell. Dengan demikian, pemahaman dotproduct sangat penting untuk mempelajari teori medan elektromagnetik. Lebih lanjut, aplikasi serupa juga ditemukan dalam mekanika fluida dan teori medan lainnya.
Aplikasi Dot Product dalam Ilmu Komputer
Grafika Komputer dan Rendering
Dalam grafika komputer, dot product merupakan operasi yang sangat sering digunakan untuk berbagai perhitungan. Pertama dan terutama, operasi ini digunakan untuk menghitung pencahayaan (lighting) dengan menentukan sudut antara vektor normal permukaan dan arah sumber cahaya. Kedua, dotproduct membantu menentukan apakah suatu permukaan menghadap kamera atau tidak (backface culling). Menariknya, jutaan operasi dotproduct dilakukan setiap detik dalam rendering real-time seperti video game. Dengan demikian, optimasi operasi ini sangat krusial untuk performa grafika.
Machine Learning dan Data Science
Dalam machine learning, dot product menjadi operasi fundamental yang mendasari banyak algoritma. Secara spesifik, neural networks menggunakan dotproduct secara masif dalam perhitungan forward propagation dan backpropagation. Selain itu, algoritma seperti k-nearest neighbors menggunakan dotproduct untuk menghitung similarity antara data points. Pada kenyataannya, banyak library machine learning modern mengoptimalkan operasi dotproduct menggunakan hardware khusus seperti GPU. Lebih lanjut, pemahaman dotproduct sangat penting untuk memahami arsitektur deep learning modern.
Aplikasi dalam komputasi:
- Pertama, perhitungan similarity dalam information retrieval
- Kedua, operasi dasar dalam neural networks
- Ketiga, algoritma rekomendasi sistem
- Keempat, pemrosesan sinyal digital
- Kelima, kompresi data dan PCA
- Keenam, computer vision dan pattern recognition
- Ketujuh, natural language processing
- Terakhir, optimasi numerik dan solver linear
Pemrosesan Sinyal dan Transformasi
Dalam pemrosesan sinyal digital, dot product digunakan untuk menghitung korelasi dan konvolusi. Secara matematis, korelasi silang antara dua sinyal dapat dihitung menggunakan serangkaian operasi dotproduct. Menariknya, operasi ini sangat penting dalam deteksi pola, kompresi audio, dan analisis frekuensi. Dengan demikian, pemahaman dotproduct sangat relevan untuk bidang telekomunikasi dan audio engineering. Lebih lanjut, transformasi Fourier yang fundamental juga melibatkan operasi yang mirip dengan dotproduct.
Metode Perhitungan Dot Product yang Efisien
Algoritma Komputasi Manual
Untuk perhitungan manual, metode paling sederhana adalah mengalikan komponen-komponen yang bersesuaian lalu menjumlahkannya. Pertama, tuliskan kedua vektor dalam bentuk komponen yang jelas. Kedua, kalikan setiap pasangan komponen yang sesuai. Ketiga, jumlahkan semua hasil perkalian untuk mendapatkan hasil akhir. Menariknya, metode ini sangat mudah dipahami dan dapat diterapkan untuk vektor dengan dimensi berapa pun. Namun demikian, untuk vektor dengan dimensi sangat besar, perhitungan manual menjadi tidak praktis.
Implementasi Komputasi dalam Program
Dalam pemrograman, dot product biasanya diimplementasikan menggunakan loop atau operasi vektor terbawaan. Sebagai contoh, dalam Python dengan NumPy, operasi ini sesederhana np.dot(a, b). Sementara itu, untuk implementasi dari nol, kita dapat menggunakan loop yang mengiterasi setiap komponen. Pada kenyataannya, library matematika modern menggunakan optimasi SIMD (Single Instruction Multiple Data) untuk mempercepat perhitungan. Lebih lanjut, GPU dapat melakukan ribuan operasi dotproduct secara paralel untuk performa maksimal.
Teknik optimasi komputasi:
- Pertama, memanfaatkan instruksi SIMD pada CPU modern
- Kedua, menggunakan parallel computing dengan GPU
- Ketiga, menerapkan cache-friendly memory access
- Keempat, memanfaatkan sparse matrix representation
- Kelima, menggunakan quantization untuk reduced precision
- Terakhir, menerapkan loop unrolling dan vectorization
Pertimbangan Numerik dan Presisi Dot Product
Dalam perhitungan numerik, ada beberapa isu yang perlu diperhatikan terkait presisi. Pertama, akumulasi error floating-point dapat terjadi ketika menjumlahkan banyak hasil perkalian. Kedua, overflow atau underflow dapat terjadi untuk vektor dengan komponen sangat besar atau sangat kecil. Oleh karena itu, algoritma numerik yang robust sering menggunakan teknik seperti Kahan summation untuk meningkatkan akurasi. Dengan demikian, pemahaman numerical stability sangat penting untuk aplikasi kritis yang memerlukan presisi tinggi.
Contoh Soal dan Pembahasan Lengkap
Contoh Soal Dasar dalam R²
Soal 1: Diberikan vektor u = (3, 4) dan v = (1, 2). Hitunglah u · v.
Pembahasan: Menggunakan rumus aljabar, kita kalikan komponen-komponen yang bersesuaian. Dengan demikian, u · v = (3)(1) + (4)(2) = 3 + 8 = 11. Hasil akhir adalah 11, yang merupakan bilangan skalar. Lebih lanjut, nilai positif ini menunjukkan bahwa kedua vektor membentuk sudut lancip.
Contoh Soal dengan Sudut
Soal 2: Jika |a| = 5, |b| = 3, dan sudut antara a dan b adalah 60°, berapakah a · b?
Pembahasan: Menggunakan rumus geometris a · b = |a| |b| cos θ. Dengan demikian, a · b = (5)(3) cos(60°) = 15 × 0.5 = 7.5. Menariknya, kita dapat menghitung dot product tanpa mengetahui komponen-komponen vektor secara eksplisit. Lebih lanjut, metode ini sangat berguna ketika informasi sudut tersedia.
Langkah-langkah penyelesaian soal:
- Pertama, identifikasi informasi yang diberikan dalam soal
- Kedua, tentukan rumus yang paling sesuai untuk digunakan
- Ketiga, substitusi nilai-nilai yang diketahui ke dalam rumus
- Keempat, lakukan perhitungan aritmatika dengan teliti
- Kelima, periksa satuan dan interpretasi hasil
- Terakhir, verifikasi jawaban dengan metode alternatif jika memungkinkan
Contoh Soal Aplikasi Fisika
Soal 3: Sebuah gaya F = (10, 5) Newton menyebabkan benda berpindah sejauh d = (3, 4) meter. Hitunglah kerja yang dilakukan.
Pembahasan: Kerja dihitung menggunakan W = F · d. Oleh karena itu, W = (10)(3) + (5)(4) = 30 + 20 = 50 Joule. Hasil ini menunjukkan total energi yang ditransfer ke benda. Menariknya, jika gaya tegak lurus perpindahan, dotproduct akan menghasilkan nol, menunjukkan tidak ada kerja yang dilakukan. Dengan demikian, formula ini secara alami menangkap konsep fisika bahwa kerja memerlukan gaya dan perpindahan searah.
Kesalahan Umum dan Cara Menghindarinya
Kesalahan Dimensi Vektor
Salah satu kesalahan paling umum adalah mencoba menghitung dot product dari dua vektor dengan dimensi berbeda. Pada kenyataannya, operasi ini tidak terdefinisi secara matematis. Sebagai contoh, vektor (1, 2, 3) tidak dapat di-dot dengan vektor (4, 5) karena memiliki panjang berbeda. Oleh karena itu, selalu pastikan kedua vektor memiliki jumlah komponen yang sama sebelum melakukan perhitungan. Lebih lanjut, dalam pemrograman, hal ini dapat menyebabkan error runtime jika tidak ditangani dengan baik.
Kesalahan Interpretasi Hasil
Kesalahan lain yang sering terjadi adalah menginterpretasikan hasil dot product sebagai vektor, padahal hasilnya adalah skalar. Lebih lanjut, beberapa mahasiswa keliru mengasosiasikan nilai besar dengan “sudut besar”, padahal nilai dotproduct bergantung pada magnitudo vektor juga. Dengan demikian, untuk membandingkan sudut antar pasangan vektor, lebih baik menggunakan cosine similarity yang dinormalisasi. Selain itu, tanda hasil (positif/negatif) harus dipahami dalam konteks sudut lancip versus tumpul.
Kesalahan yang harus dihindari:
- Pertama, mengasumsikan hasil berupa vektor bukan skalar
- Kedua, menggunakan vektor dengan dimensi tidak cocok
- Ketiga, salah menginterpretasi nilai nol
- Keempat, mengacaukan dotproduct dengan cross product
- Kelima, mengabaikan aturan komutatif dalam urutan
- Keenam, lupa mempertimbangkan tanda hasil
- Terakhir, tidak memvalidasi hasil perhitungan
Kesalahan Perhitungan Numerik
Dalam komputasi numerik, kesalahan pembulatan dapat terakumulasi terutama untuk vektor dengan banyak komponen. Pada dasarnya, floating-point arithmetic tidak sempurna dan dapat menyebabkan hasil yang sedikit berbeda dari nilai eksak. Oleh karena itu, ketika membandingkan hasil dotproduct dengan nol (untuk tes ortogonalitas), gunakan threshold kecil seperti 1e-10 daripada perbandingan eksak. Lebih lanjut, untuk aplikasi kritis, pertimbangkan menggunakan aritmatika presisi tinggi atau algoritma numerik yang lebih stabil.
Generalisasi dan Topik Lanjutan
Inner Product dan Ruang Hilbert
Dot product adalah contoh khusus dari konsep yang lebih umum yaitu inner product atau hasil kali dalam. Secara matematis, inner product adalah fungsi bilinear yang memenuhi sifat-sifat tertentu seperti positive definiteness dan conjugate symmetry. Menariknya, konsep ini dapat digeneralisasi ke ruang vektor abstrak dan bahkan ruang fungsi. Dengan demikian, dotproduct standar hanyalah satu dari banyak kemungkinan inner product yang dapat didefinisikan. Lebih lanjut, teori ruang Hilbert yang menjadi fondasi mekanika kuantum dibangun di atas konsep inner product yang digeneralisasi ini.
Tensor Product dan Operasi Tingkat Tinggi
Dalam matematika lanjutan, ada generalisasi dari dot product ke dimensi yang lebih tinggi yaitu tensor product. Secara konseptual, tensor product memperluas ide perkalian vektor ke objek matematika yang lebih kompleks. Pada kenyataannya, tensor sangat penting dalam relativitas umum dan teori medan kuantum. Dengan demikian, pemahaman solid tentang dotproduct menjadi stepping stone untuk mempelajari aljabar tensor. Lebih lanjut, machine learning modern seperti tensor decomposition juga memanfaatkan konsep-konsep ini.
Topik lanjutan terkait:
- Pertama, inner product spaces dan normed spaces
- Kedua, functional analysis dan operator theory
- Ketiga, tensor algebra dan multilinear maps
- Keempat, kernel methods dalam machine learning
- Kelima, Riemannian geometry dan metric tensors
- Terakhir, quantum mechanics dan bra-ket notation
Aplikasi dalam Ruang Dimensi Tinggi
Dalam era big data dan machine learning, bekerja dengan vektor berdimensi sangat tinggi (ratusan ribu hingga jutaan dimensi) menjadi umum. Menariknya, dot product tetap menjadi operasi fundamental bahkan dalam high-dimensional spaces ini. Namun demikian, ada fenomena unik seperti curse of dimensionality yang perlu dipahami. Oleh karena itu, teknik seperti dimensionality reduction dan kernel tricks dikembangkan untuk bekerja efektif di ruang dimensi tinggi. Lebih lanjut, pemahaman dotproduct sangat penting untuk memahami algoritma seperti PCA dan support vector machines.
Dot Product dalam Konteks Interdisipliner
Aplikasi dalam Ekonomi dan Statistika
Dalam ekonomi, dot product digunakan untuk menghitung nilai total dari portofolio investasi. Sebagai contoh, jika vektor q merepresentasikan kuantitas aset dan p merepresentasikan harga, maka nilai total adalah p · q. Sementara itu, dalam statistika, dotproduct digunakan dalam perhitungan kovariansi dan korelasi. Pada kenyataannya, konsep projection yang didasarkan pada dotproduct mendasari regresi linear. Dengan demikian, pemahaman dotproduct sangat relevan untuk analisis data dan ekonometrika.
Aplikasi dalam Bioinformatika
Dalam bioinformatika, dot product digunakan untuk mengukur similarity antara sekuens biologis yang direpresentasikan sebagai vektor. Secara khusus, teknik seperti sequence alignment sering memanfaatkan operasi yang mirip dengan dotproduct. Menariknya, penelitian protein structure prediction juga menggunakan inner products dalam berbagai tahap komputasi. Lebih lanjut, analisis gene expression data dengan teknik seperti clustering juga memanfaatkan similarity measures yang didasarkan pada dot product.
Bidang-bidang penerapan:
- Pertama, ekonomi dan analisis portofolio investasi
- Kedua, statistika dan machine learning
- Ketiga, bioinformatika dan computational biology
- Keempat, rekayasa sipil dan analisis struktur
- Kelima, robotika dan computer vision
- Keenam, astronomi dan analisis data astronomis
- Ketujuh, chemoinformatics dan drug discovery
- Terakhir, climate science dan modeling atmosfer
Aplikasi dalam Rekayasa dan Desain
Dalam rekayasa mesin, dot product digunakan untuk menganalisis tegangan dan regangan dalam material. Secara spesifik, komponen tegangan dalam arah tertentu dapat dihitung menggunakan dot product dengan vektor normal permukaan. Selain itu, dalam desain CAD (Computer-Aided Design), dotproduct membantu menentukan visibilitas permukaan dan perhitungan pencahayaan. Pada kenyataannya, hampir semua software rekayasa modern menggunakan operasi vektor termasuk dotproduct secara ekstensif. Dengan demikian, insinyur perlu memahami konsep ini untuk menggunakan tools modern secara efektif.
Rangkuman dan Kesimpulan Dot Product
Dot product merupakan operasi fundamental dalam aljabar linear yang mengambil dua vektor dan menghasilkan nilai skalar. Operasi ini memiliki dua representasi ekuivalen: bentuk aljabar yang menghitung jumlah hasil kali komponen, dan bentuk geometris yang melibatkan magnitudo vektor serta sudut di antaranya. Menariknya, kedua representasi ini memberikan insight berbeda namun sama-sama penting untuk pemahaman komprehensif. Lebih lanjut, dotproduct memiliki sifat-sifat aljabar seperti komutatif, distributif, dan linear yang membuatnya sangat berguna dalam manipulasi matematika.
Dari perspektif geometris, dot product memungkinkan kita untuk menghitung proyeksi vektor, menentukan sudut antara vektor, dan mengidentifikasi ortogonalitas. Aplikasinya sangat luas, mulai dari perhitungan kerja dalam fisika mekanika, rendering dalam grafika komputer, hingga algoritma pembelajaran mesin yang kompleks. Pada kenyataannya, jutaan operasi dotproduct dilakukan setiap detik dalam aplikasi modern seperti game engines dan deep learning frameworks. Dengan demikian, menguasai konsep ini bukan hanya penting untuk akademis tetapi juga untuk praktik profesional di berbagai bidang STEM.
Bagi mahasiswa, pemahaman mendalam tentang dotproduct membuka pintu untuk mempelajari topik-topik lanjutan seperti inner product spaces, tensor algebra, dan functional analysis. Lebih lanjut, kemampuan menghitung dan mengaplikasikan dot product dengan benar sangat penting untuk sukses dalam mata kuliah aljabar linear, kalkulus vektor, fisika, dan ilmu komputer. Pada akhirnya, dotproduct adalah salah satu konsep matematika yang tampak sederhana namun memiliki kedalaman dan aplikasi yang luar biasa luas dalam sains modern dan teknologi.
Baca juga konten dengan artikel terkait tentang: Pengetahuan
Baca juga artikel lainnya: Jaringan Komputer: Pengertian, Jenis, Topologi, dan Komponen