JAKARTA, studyinca.ac.id – Geometri bidang ruang adalah salah satu cabang penting dalam matematika yang membahas bentuk tiga dimensi, seperti kubus, balok, prisma, limas, tabung, kerucut, dan bola. Cabang ilmu ini tidak hanya dipelajari di sekolah, tetapi juga memiliki peranan besar dalam dunia arsitektur, teknik, seni, hingga teknologi modern. Artikel ini akan membahas Geometri Bidang Ruang secara lengkap dan santai, namun tetap menggunakan bahasa yang sopan dan mudah dipahami.
Mengenal Apa Itu Geometri Bidang Ruang
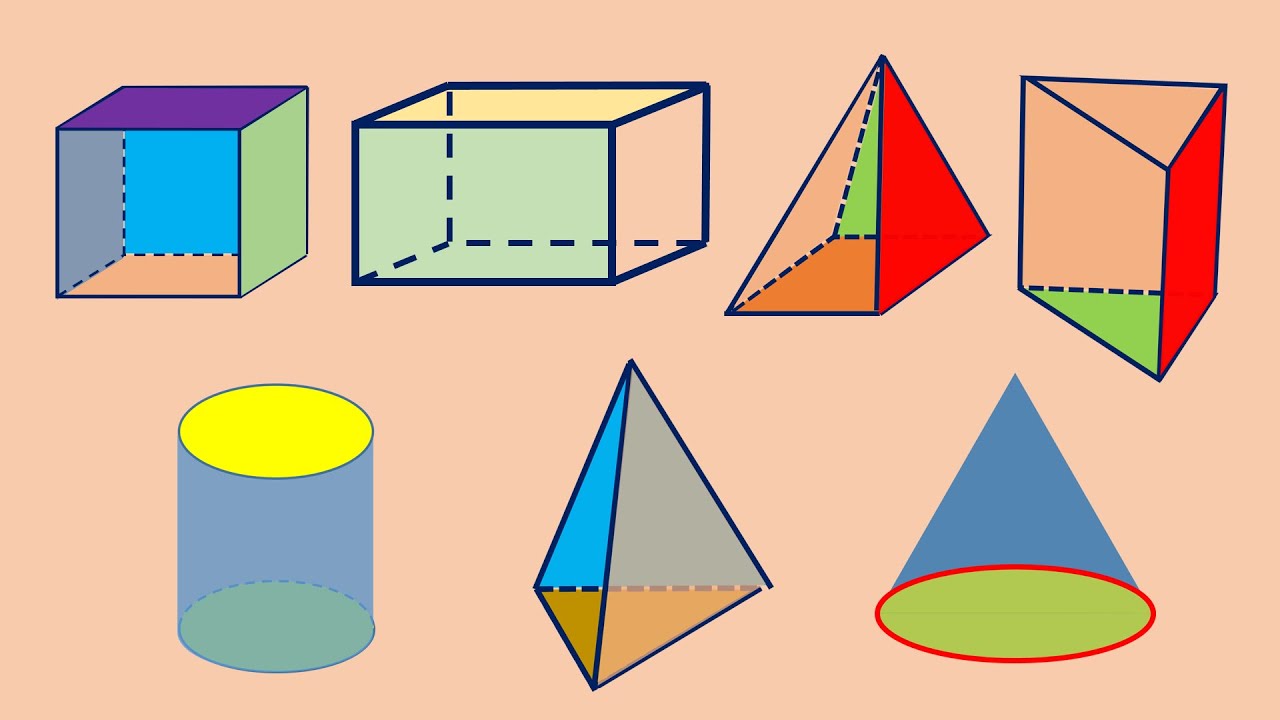
Sebelum masuk lebih dalam, mari kita pahami terlebih dahulu apa yang dimaksud dengan geometri bidang ruang.
Secara sederhana, geometri bidang ruang merupakan bagian dari matematika yang mempelajari bangun tiga dimensi (3D) yang memiliki panjang, lebar, dan tinggi.
Contohnya bisa kita temukan di sekitar kita, seperti kotak sepatu (balok), dadu (kubus), tenda (limas), atau bola sepak (bola).
Setiap bangun ruang memiliki volume dan luas permukaan, yang menjadi ciri khasnya dibandingkan dengan bangun datar.
Sejarah dan Perkembangan Geometri Bidang Ruang
Ilmu geometri telah dikenal sejak zaman Mesir Kuno. Bangsa Mesir menggunakan konsep dasar geometri untuk membangun piramida dan mengukur tanah setelah banjir Sungai Nil. Namun, Geometri Bidang Ruang mulai berkembang pesat setelah diperkenalkan oleh Euclid, seorang matematikawan Yunani kuno yang dikenal sebagai “Bapak Geometri”.
Euclid menyusun The Elements, buku yang menjelaskan konsep titik, garis, bidang, dan ruang.
Dari sinilah kemudian lahir berbagai teori dan rumus tentang volume serta luas permukaan bangun ruang yang kita kenal hingga saat ini.
Unsur-Unsur dalam Geometri Bidang Ruang
Setiap bangun ruang memiliki beberapa unsur penting yang menjadi dasar dalam mempelajarinya. Berikut unsur-unsurnya:
-
Titik (Vertex): Titik adalah sudut tempat dua atau lebih rusuk bertemu.
-
Rusuk (Edge): Garis lurus yang menghubungkan dua titik sudut.
-
Bidang (Face): Permukaan datar yang membentuk sisi luar bangun ruang.
-
Diagonal Ruang: Garis yang menghubungkan dua titik sudut yang tidak terletak pada bidang yang sama.
Memahami unsur-unsur ini penting agar kita bisa mengenali bentuk ruang secara menyeluruh sebelum menghitung luas atau volumenya.
Jenis-Jenis Bangun dalam Geometri Bidang Ruang
Dalam geometri bidang ruang, terdapat berbagai macam bentuk tiga dimensi dengan karakteristik dan rumus yang berbeda. Berikut penjelasan beberapa di antaranya.
a. Kubus
Geometri bidang ruang Kubus adalah bangun ruang yang semua sisinya berbentuk persegi dan memiliki panjang rusuk yang sama.
Rumus volume: V = s³
Rumus luas permukaan: L = 6 × s²
Contoh benda berbentuk kubus adalah dadu, kotak tisu, dan rubik.
b. Balok
Geometri bidang ruang Balok memiliki enam sisi berbentuk persegi panjang. Panjang, lebar, dan tinggi balok dapat berbeda.
Rumus volume: V = p × l × t
Rumus luas permukaan: L = 2 × (pl + pt + lt)
Contoh benda berbentuk balok adalah lemari, kulkas, dan kotak sepatu.
c. Prisma
Geometri bidang ruang Prisma memiliki dua bidang alas yang sejajar dan kongruen (sama bentuk dan ukuran).
Rumus volume: V = luas alas × tinggi
Rumus luas permukaan: L = (2 × luas alas) + (keliling alas × tinggi)
Contohnya seperti atap rumah atau kemasan susu segitiga.
d. Limas
Geometri bidang ruang Limas memiliki alas berbentuk segi-n dan sisi tegak berbentuk segitiga yang bertemu di satu titik puncak.
Rumus volume: V = ⅓ × luas alas × tinggi
Rumus luas permukaan: Jumlah luas alas dan seluruh sisi tegak.
Bangun seperti piramida Mesir merupakan contoh limas segi empat.
e. Tabung
Tabung adalah bangun ruang dengan dua lingkaran sejajar yang dihubungkan oleh selimut berbentuk persegi panjang melingkar.
Rumus volume: V = π × r² × t
Rumus luas permukaan: L = 2πr(r + t)
Contoh benda tabung adalah kaleng, pipa, dan gelas.
f. Kerucut
Kerucut memiliki alas berbentuk lingkaran dan satu titik puncak di atasnya.
Rumus volume: V = ⅓ × π × r² × t
Rumus luas permukaan: L = πr (r + s), di mana s = garis pelukis.
Contoh benda berbentuk kerucut adalah topi ulang tahun atau corong.
g. Bola
Bola adalah bangun ruang yang memiliki permukaan lengkung sempurna.
Rumus volume: V = ⁴⁄₃ × π × r³
Rumus luas permukaan: L = 4πr²
Contoh bola tentu sangat banyak, seperti bola basket, globe, atau lampu bulat.
Hubungan Teorema Pythagoras dalam Geometri Bidang Ruang
Dalam geometri bidang ruang, Teorema Pythagoras sering digunakan untuk menghitung diagonal ruang.
Misalnya, dalam balok dengan panjang p, lebar l, dan tinggi t, diagonal ruang dapat dihitung dengan rumus:
d = √(p² + l² + t²)
Hubungan ini penting karena membantu menentukan jarak antara dua titik dalam ruang tiga dimensi.
Seperti pada bangunan arsitektur modern, perhitungan diagonal ruang digunakan untuk menilai kestabilan dan presisi struktur.
Aplikasi Geometri Bidang Ruang dalam Kehidupan Nyata
Geometri bidang ruang tidak hanya menjadi teori dalam pelajaran sekolah, tetapi juga memiliki banyak penerapan dalam kehidupan nyata. Beberapa di antaranya adalah:
-
Dalam Arsitektur dan Desain Interior:
Bangunan rumah, gedung, dan jembatan dibuat berdasarkan perhitungan volume dan luas permukaan agar konstruksi kuat dan efisien. -
Dalam Dunia Teknologi:
Aplikasi pemodelan 3D dan desain grafis menggunakan prinsip geometri ruang untuk menciptakan visualisasi yang realistis.
Bahkan dalam game seperti Food Truck Chef Game, pengembang memanfaatkan geometri ruang untuk membuat tampilan kendaraan dan peralatan dapur tampak nyata secara tiga dimensi. -
Dalam Dunia Industri:
Produsen perlu menghitung volume wadah atau tangki agar sesuai dengan kapasitas produksi. -
Dalam Dunia Penerbangan:
Pilot dan insinyur menggunakan konsep ruang untuk menghitung jarak, lintasan, dan orientasi pesawat di udara.
Rumus Penting dalam Geometri Bidang Ruang
Agar mudah diingat, berikut beberapa rumus umum yang sering digunakan:
| Bangun Ruang | Volume | Luas Permukaan |
|---|---|---|
| Kubus | s³ | 6 × s² |
| Balok | p × l × t | 2(pl + pt + lt) |
| Prisma | luas alas × tinggi | 2 × luas alas + keliling alas × tinggi |
| Limas | ⅓ × luas alas × tinggi | luas alas + luas sisi tegak |
| Tabung | πr²t | 2πr(r + t) |
| Kerucut | ⅓πr²t | πr(r + s) |
| Bola | ⁴⁄₃πr³ | 4πr² |
Rumus-rumus ini menjadi dasar dalam menghitung bentuk tiga dimensi dan sering digunakan dalam bidang konstruksi, pendidikan, hingga industri kreatif.
Perbedaan Antara Bidang Datar dan Bidang Ruang
Perbedaan mendasar antara bidang datar dan bidang ruang terletak pada dimensi yang dimiliki.
Bidang datar hanya memiliki dua dimensi (panjang dan lebar), sedangkan bidang ruang memiliki tiga dimensi (panjang, lebar, dan tinggi).
| Aspek | Bidang Datar | Bidang Ruang |
|---|---|---|
| Dimensi | 2D | 3D |
| Ciri Utama | Luas | Volume |
| Contoh | Persegi, Segitiga, Lingkaran | Kubus, Balok, Tabung |
| Unsur | Titik, Garis, Bidang | Titik, Rusuk, Bidang, Ruang |
Tips Memahami dengan Mudah
Bagi sebagian orang, menghitung volume atau luas permukaan bangun ruang bisa terasa rumit. Namun, dengan beberapa tips berikut, konsep ini bisa lebih mudah dipahami:
-
Gunakan benda nyata di sekitar. Misalnya, gunakan kotak susu untuk memvisualisasikan balok.
-
Pelajari melalui gambar 3D atau model fisik.
-
Pahami hubungan antar sisi dan diagonal.
-
Gunakan warna berbeda untuk membedakan bidang-bidang dalam bangun.
-
Latihan soal secara rutin.
Dengan latihan teratur dan memahami logikanya, rumus-rumus geometri tidak akan terasa membingungkan.
Pentingnya di Dunia Modern
Di era modern, pemahaman tentang geometri bidang ruang sangat dibutuhkan, terutama di bidang desain digital, arsitektur, dan teknologi 3D printing.
Bahkan dunia pendidikan kini menggunakan pendekatan visualisasi interaktif untuk membantu siswa memahami konsep ruang dengan lebih baik.
Penerapan geometri bidang ruang juga sangat terasa di bidang seni dan film animasi, di mana konsep volume, perspektif, dan pencahayaan digunakan untuk menciptakan kesan realistis pada objek virtual.
Antara Teori dan Realitas
Dari penjelasan di atas, kita dapat melihat bahwa geometri bidang ruang tidak hanya sekadar teori dalam buku pelajaran, tetapi juga menjadi pondasi penting dalam berbagai aspek kehidupan manusia.
Dengan memahami konsep volume, luas permukaan, serta hubungan antar bidang, kita dapat menciptakan sesuatu yang lebih presisi dan fungsional, baik dalam dunia akademik maupun profesional.
Mulai dari desain rumah, pembuatan alat transportasi, hingga game dan teknologi digital — semuanya tidak lepas dari penerapan konsep geometri bidang ruang.
Belajar geometri berarti belajar memahami dunia secara lebih terukur dan logis. Dengan pemahaman yang baik, kita dapat melihat bahwa setiap bentuk di sekitar kita memiliki harmoni matematika yang indah.
Temukan informasi lengkapnya Tentang: Pengetahuan
Baca Juga Artikel Berikut: Hukum Archimedes Dasar: Panduan Lengkap Memahami Gaya Apung dan Aplikasinya

