Jajar Genjang: Bentuk Sederhana dengan Konsep Matematika

JAKARTA, studyinca.ac.id – Dalam pelajaran geometri, ada bentuk yang sering terlihat sepele namun sesungguhnya sangat filosofis: jajar genjang. Ia tampak seperti persegi panjang yang dimiringkan, tetapi di balik kemiringannya tersimpan prinsip keseimbangan dan keteraturan. Bentuk ini mengajarkan bahwa tidak semua hal yang miring itu salah — terkadang, kemiringan justru menunjukkan arah baru yang tetap selaras dengan logika matematika.

Jajargenjang menjadi salah satu konsep dasar dalam geometri yang diajarkan sejak sekolah dasar. Namun, seiring waktu, banyak yang lupa bahwa bangun datar ini memiliki peran besar dalam berbagai bidang, dari arsitektur hingga fisika. Untuk memahami ruang, gaya, bahkan gerakan benda, kita perlu memahami bagaimana garis sejajar bekerja, dan di sanalah jajargenjang menjadi model visual terbaik.

Definisi dan Sifat Dasar Jajar Genjang

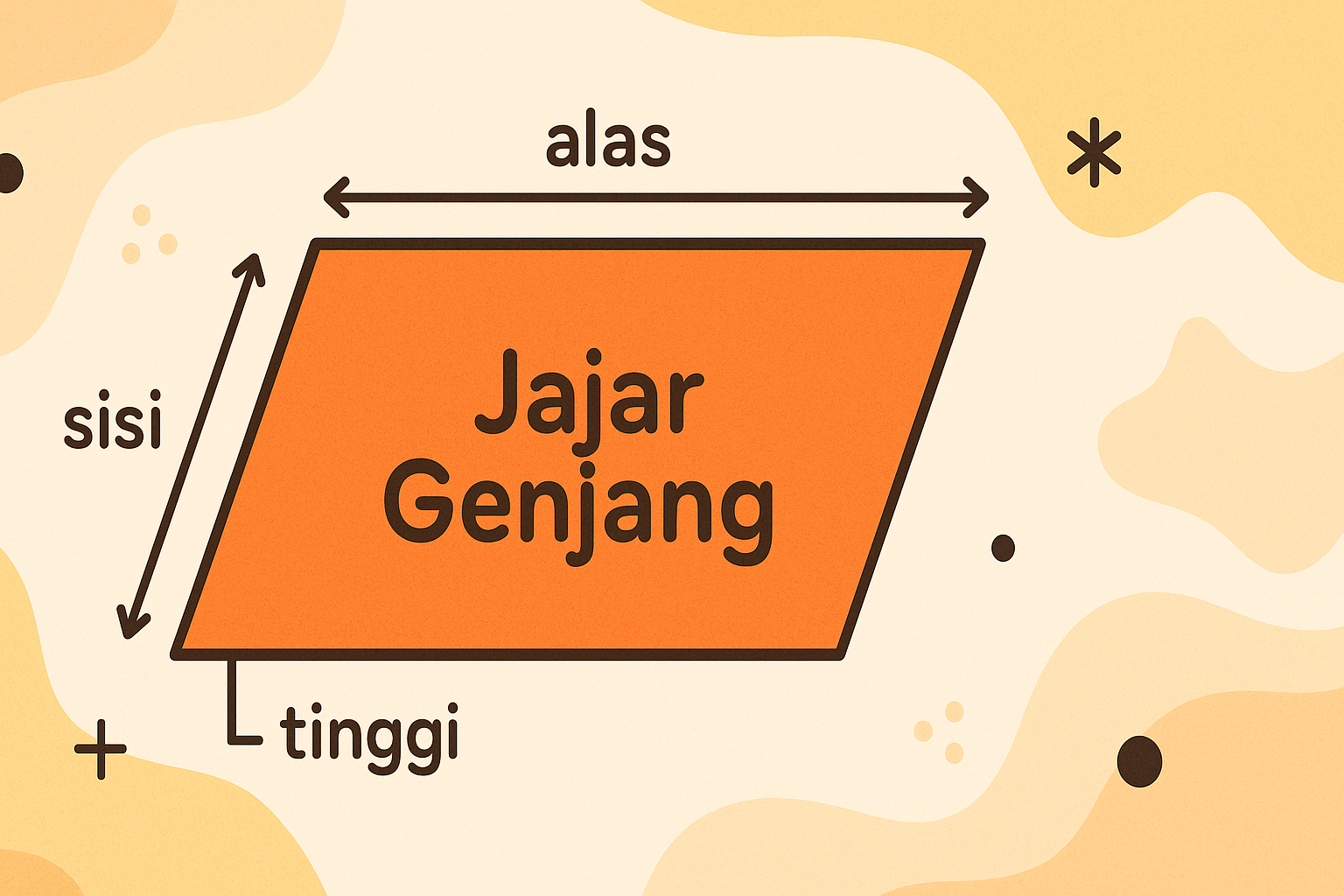
Secara sederhana, jajar genjang adalah bangun datar dua dimensi yang memiliki dua pasang sisi berhadapan yang sejajar dan sama panjang. Kata “jajar” berarti sejajar, sedangkan “genjang” berasal dari istilah lama yang berarti miring. Jadi, sesuai namanya, jajargenjang adalah bentuk sejajar yang tidak tegak lurus, tapi tetap seimbang. Berikut adalah sifat-sifat utama dari jajargenjang:

1. Memiliki dua pasang sisi yang sejajar dan sama panjang.
   Sisi yang berhadapan selalu sejajar, menandakan keteraturan arah.

2. Sudut yang berhadapan sama besar.
   Jika satu sudutnya 60°, maka sudut berlawanan juga 60°.

3. Sudut bersebelahan saling melengkapi hingga 180°.
   Artinya, jajargenjang selalu menjaga keseimbangan sudut di setiap titiknya.

4. Diagonal saling membagi dua bagian sama panjang.
   Ini membuktikan adanya simetri internal yang tidak tampak secara visual.

Dengan sifat-sifat tersebut, jajargenjang menunjukkan harmoni antara bentuk dan logika — sesuatu yang sangat esensial dalam studi geometri.

Rumus Luas dan Keliling Jajar Genjang

Dalam matematika, rumus jajar genjang sering digunakan untuk menghitung dua hal: luas dan keliling.

1. Luas Jajar Genjang
Rumus luas ditulis sebagai:

$$L=a\times t$$

Keterangan:

• L = luas

• a = panjang alas

• t = tinggi (jarak tegak lurus antara dua sisi sejajar)

Contoh:
Jika alas = 10 cm dan tinggi = 6 cm, maka:
L = 10 × 6 = 60 cm²

2. Keliling JajarGenjang
Rumus keliling ditulis sebagai:

$$K=2\times (a+b)$$

Keterangan:

• K = keliling

• a = panjang sisi alas

• b = panjang sisi miring

Contoh:
Jika a = 8 cm dan b = 5 cm, maka:
K = 2 × (8 + 5) = 26 cm

Rumus ini sederhana, tapi memiliki makna mendalam. Ia menunjukkan bahwa dalam keseimbangan, panjang dan tinggi selalu saling melengkapi — tanpa salah satunya, tidak ada bentuk yang utuh.

Hubungan Jajar Genjang dengan Bangun Datar Lain

Menariknya, jajar genjang memiliki hubungan erat dengan beberapa bentuk geometri lainnya. Ia bisa dianggap sebagai hasil transformasi dari persegi panjang — seperti bayangan yang bergeser, bukan berubah bentuk.

• Persegi Panjang vs. Jajar Genjang
  Perbedaannya hanya pada sudut. Persegi panjang memiliki sudut 90°, sedangkan jajargenjang tidak. Namun luasnya tetap dihitung dengan cara yang sama: alas dikali tinggi.

• Belah Ketupat dan JajarGenjang
  Belah ketupat adalah jajargenjang dengan semua sisi sama panjang.
  Ia menunjukkan versi “sempurna” dari kesimetrian jajargenjang.

• Trapesium dan JajarGenjang
  Trapesium hanya memiliki satu pasang sisi sejajar, sedangkan jajargenjang punya dua. Ini menjadikan jajargenjang bentuk yang lebih stabil dan teratur secara geometri.

Dengan kata lain, jajargenjang adalah bentuk dasar yang menjadi penghubung antara bentuk-bentuk datar lain — fondasi dari geometri bidang.

Konsep Transformasi dan Vektor pada Jajar Genjang

Dalam pelajaran matematika tingkat lanjut, jajar genjang juga menjadi model visual penting untuk memahami konsep vektor. Jika dua vektor berawal dari titik yang sama, maka hasil penjumlahan vektor tersebut membentuk jajargenjang. Inilah yang disebut Aturan JajarGenjang (Parallelogram Law) dalam fisika dan matematika. Misalnya, jika dua gaya bekerja pada satu titik dengan arah berbeda, maka resultannya adalah diagonal dari jajargenjang yang dibentuk oleh kedua gaya itu. Secara simbolik, jika dua vektor adalah A dan B, maka resultan R bisa ditulis sebagai:

R⃗=A⃗+B⃗\vec{R} = \vec{A} + \vec{B}R=A+B

Aturan ini menunjukkan bahwa jajar genjang bukan hanya bentuk, tetapi juga konsep abstrak tentang keseimbangan gaya dan arah. Ia mengajarkan bahwa dua kekuatan yang tampak bertentangan bisa menghasilkan satu arah baru bila bekerja bersama.

Makna Filosofis di Balik Bentuk Jajar Genjang

Meski lahir dari matematika, jajar genjang menyimpan filosofi menarik tentang kehidupan. Dua garis sejajar yang tak pernah bertemu bisa diartikan sebagai prinsip dan realitas — berjalan berdampingan tanpa bertabrakan. Dalam konteks sosial, jajargenjang bisa diibaratkan sebagai simbol kerja sama. Setiap sisi memiliki peran yang berbeda, tapi semuanya membentuk kesatuan yang seimbang. Sudut yang berhadapan tidak identik dalam arah, tapi setara dalam fungsi.

Filosofi ini sering digunakan dalam dunia arsitektur dan seni rupa. Bentuk jajargenjang menjadi simbol keseimbangan dinamis — struktur yang stabil, tapi tidak kaku. Itulah sebabnya, banyak desain modern menggunakan pola jajargenjang sebagai motif estetika dan simbol harmoni.

Aplikasi JajarGenjang dalam Kehidupan Sehari-hari

Konsep jajar genjang tidak berhenti di papan tulis sekolah. Bentuk ini sering ditemui dalam kehidupan nyata, bahkan tanpa disadari.

1. Desain Arsitektur dan Konstruksi
   Banyak jembatan, gedung, dan atap menggunakan struktur jajargenjang untuk menahan gaya tekan dan tarik.
   Kemiringannya memberi stabilitas terhadap tekanan angin dan beban.

2. Bidang Seni dan Desain Grafis
   Dalam dunia desain, pola jajargenjang menciptakan kesan gerak dan kedalaman visual.
   Logo, tekstur, dan tata letak sering memanfaatkan bentuk ini untuk menciptakan kesan dinamis.

3. Teknik Mesin dan Fisika
   Sistem suspensi mobil dan engsel pintu menggunakan prinsip kerja jajargenjang agar pergerakan tetap sejajar dan stabil.

4. Perhitungan Tanah dan Peta
   Dalam bidang geodesi, bentuk lahan yang miring atau tidak beraturan sering dikonversi ke model jajargenjang agar mudah dihitung luasnya.

Dari dunia seni hingga teknik, jajargenjang membuktikan bahwa bentuk sederhana bisa memiliki dampak besar bila dipahami dengan benar.

Cara Menggambar Jajar Genjang dengan Tepat

Menggambar jajar genjang membutuhkan ketelitian karena kemiringannya harus konsisten. Langkah-langkahnya sederhana:

1. Gambar satu garis lurus sebagai alas.

2. Dari setiap ujung alas, gambar dua garis sejajar dengan panjang yang sama tetapi miring pada sudut tertentu.

3. Hubungkan kedua ujung atas garis miring, dan bentuk jajargenjang pun selesai.

Jika ingin memastikan hasilnya akurat, gunakan penggaris sejajar atau busur derajat untuk menentukan kemiringan sudut. Kesalahan kecil pada sudut bisa mengubah bentuk menjadi trapesium.

JajarGenjang dalam Pendidikan: Lebih dari Sekadar Rumus

Bagi guru matematika, jajar genjang bukan sekadar topik ajar, tapi alat untuk melatih logika berpikir siswa. Konsep ini membantu anak memahami bahwa keseimbangan tidak selalu berarti kesamaan. Ia juga menjadi pengantar bagi pelajaran yang lebih kompleks, seperti vektor, gaya, dan matriks. Ketika siswa belajar menggambar dan menghitung luas jajargenjang, mereka sebenarnya sedang mempraktikkan prinsip berpikir sistematis — kemampuan yang akan berguna di luar dunia matematika. Dengan pendekatan naratif dan visual, pelajaran tentang jajargenjang bisa menjadi pintu masuk untuk mencintai geometri, bukan sekadar menghafal rumusnya.

Kesalahan Umum dalam Memahami Jajar Genjang

Beberapa kesalahan umum sering terjadi saat siswa belajar tentang jajar genjang:

1. Menganggap tinggi selalu sama dengan sisi miring.
   Padahal tinggi adalah jarak tegak lurus antara dua sisi sejajar, bukan panjang sisi.

2. Salah mengukur alas dan tinggi.
   Banyak siswa keliru mengambil sisi miring sebagai alas, padahal alas selalu menjadi salah satu sisi sejajar.

3. Mengira semua sisi sama panjang.
   Ini hanya berlaku untuk belah ketupat, bukan untuk jajargenjang umum.

4. Lupa bahwa diagonal tidak sama panjang.
   Tidak seperti persegi panjang, diagonal jajargenjang berbeda panjang tetapi tetap saling membagi dua.

Dengan memahami kesalahan ini, pengajaran jajargenjang bisa menjadi lebih efektif dan logis.

Penutup: Kesederhanaan yang Penuh Makna

Jajar genjang mengajarkan bahwa bentuk paling sederhana sekalipun bisa menyimpan kedalaman konsep yang luar biasa. Ia bukan hanya soal garis dan sudut, tetapi tentang keseimbangan, arah, dan keteraturan. Dua sisi sejajar yang tak pernah bertemu mengingatkan kita bahwa harmoni tidak selalu berarti kesamaan. Dalam logika maupun kehidupan, jajargenjang menjadi simbol bahwa keindahan bisa muncul dari keselarasan antara kemiringan dan keteguhan. Matematika tidak selalu dingin dan abstrak — kadang, ia justru menjadi cara alam berbicara tentang keseimbangan yang indah. Dan jajargenjang adalah salah satu bahasa geometrinya yang paling elegan.

Baca juga konten dengan artikel terkait tentang:  Pengetahuan

Baca juga artikel lainnya: Ikatan Ion: Pembentukan, Ciri, dan Perannya