Kalau saya ditanya bangun ruang apa yang pertama kali saya pahami waktu SD, jawabannya pasti kubus. Bukan karena bentuknya paling sederhana, tapi karena di sekeliling saya banyak benda berbentuk ku bus. Mulai dari kotak kado kecil, rubik, sampai kotak makanan plastik di dapur. Dari situ saya sadar bahwa mengenal bangun ruang seperti kubus bukan sekadar pelajaran di buku, tapi benar-benar bagian dari kehidupan sehari-hari.
Makanya, waktu saya harus menjelaskan soal volume kubus ke adik saya, saya tahu pendekatannya harus sederhana dan visual. Tidak pakai rumus yang bikin dahi berkerut, tapi dengan logika dan contoh nyata. Karena menurut saya, belajar matematika itu lebih mudah kalau kita mengaitkannya langsung dengan apa yang kita lihat dan sentuh setiap hari.
Apa Itu Kubus?

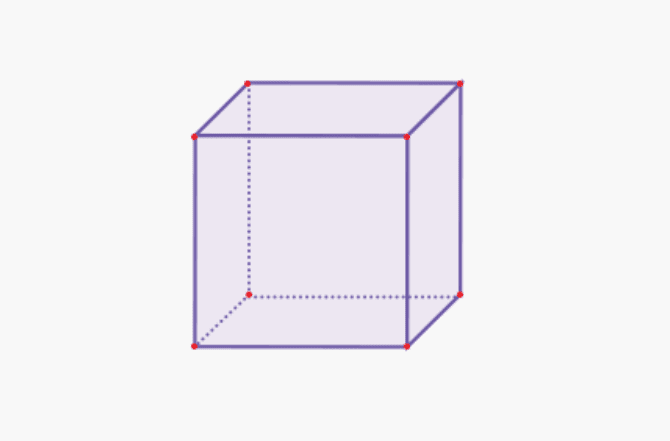
Kubus adalah bangun ruang tiga dimensi yang memiliki enam sisi berbentuk persegi yang sama besar. Artinya, semua panjang rusuknya sama. Ku bus adalah salah satu contoh prisma segi empat, dan dalam matematika, bentuk ini tergolong bangun ruang beraturan.
Ciri-Ciri Kubus:
-
Memiliki 6 sisi yang sama bentuk dan ukurannya (persegi)
-
Memiliki 12 rusuk yang panjangnya sama
-
Memiliki 8 titik sudut
-
Semua sudutnya siku-siku (90 derajat)
-
Memiliki diagonal sisi, diagonal ruang, dan bidang diagonal
Beberapa benda sehari-hari berbentuk kubus:
-
Dadu
-
Rubik’s cube
-
Kotak kecil penyimpanan
-
Speaker mini atau kemasan sabun
Dengan memahami ciri-cirinya, kita bisa membedakan kubus dari bangun ruang lain seperti balok, prisma, atau limas.
Rumus Volume Kubus
Rumus paling penting yang harus dikuasai saat belajar tentang ku bus adalah rumus volume. Volume menunjukkan seberapa besar ruang yang bisa diisi dalam suatu benda kubus.
Rumus Volume Kubus:
V = s × s × s
atau
V = s³
Keterangan:
-
V adalah volume kubus
-
s adalah panjang salah satu rusuk kubus
Satuan volume biasanya adalah satuan panjang kubik, seperti cm³, m³, atau mm³ tergantung satuan panjang rusuknya.
Contoh Perhitungan:
Jika panjang rusuk ku bus adalah 5 cm, maka:
V = 5 × 5 × 5 = 125 cm³
Artinya, ku bus itu mampu menampung volume sebesar 125 cm kubik.
Mengapa Volume Kubus Itu Penting?
Saya pernah menggunakan rumus ini secara nyata ketika membantu menata ulang lemari dapur. Kami membeli kotak penyimpanan baru dan ingin tahu apakah cukup untuk menyimpan stok makanan kering seperti biskuit atau gula.
Dengan menghitung volume kotak (yang bentuknya ku bus), kami bisa memperkirakan kapasitas isinya. Dan ternyata, matematika bukan hanya soal angka di kertas, tapi juga alat bantu dalam membuat keputusan praktis di rumah.
Selain itu, volume kubus penting dalam berbagai bidang:
-
Arsitektur: Menghitung kapasitas ruang dalam bangunan
-
Logistik: Menghitung muatan dalam peti kemas
-
Sains: Mengukur volume zat padat
-
Industri: Desain kemasan dan produksi barang
Permukaan Kubus dan Rumus Luasnya
Selain volume, kita juga perlu paham luas permukaan kubus. Ini penting ketika kita ingin tahu seberapa banyak bahan (misalnya cat, kertas, plastik) yang dibutuhkan untuk menutupi seluruh bagian ku bus.
Rumus Luas Permukaan Kubus:
L = 6 × s²
Keterangan:
-
L adalah luas permukaan
-
s adalah panjang rusuk kubus
Karena ada 6 sisi persegi yang semuanya sama, tinggal kalikan luas satu sisi dengan enam.
Contoh Soal:
Jika rusuk kubus = 4 cm, maka:
L = 6 × 4² = 6 × 16 = 96 cm²
Jadi, permukaan kubus itu seluas 96 cm persegi.
Bedanya Kubus dan Balok
Banyak yang masih bingung membedakan antara ku bus dan balok. Padahal keduanya mirip, tapi tidak sama.
| Aspek | Kubus | Balok |
|---|---|---|
| Sisi | 6 sisi sama besar (persegi) | 6 sisi bisa berbeda (persegi panjang) |
| Rusuk | Semua panjangnya sama | Rusuk bisa berbeda panjang |
| Contoh | Dadu, kotak rubik | Buku, lemari, kotak tisu |
Dengan perbandingan ini, mudah untuk mengenali keduanya, bahkan untuk anak SD sekalipun.
Menghitung Volume dalam Kehidupan Nyata
Contoh 1:
Kamu punya kotak hadiah berbentuk ku bus dengan panjang sisi 10 cm.
Berapa volume kotak tersebut?
V = 10 × 10 × 10 = 1000 cm³
Jadi, kamu bisa mengisi isi kotak itu dengan barang hingga volume 1000 cm kubik.
Contoh 2:
Sebuah tempat es batu berbentuk ku bus memiliki rusuk 3 cm. Ada 10 kotak es batu.
Berapa volume total es batu?
Volume satu kotak es: V = 3³ = 27 cm³
Total: 10 × 27 = 270 cm³
Ini contoh sederhana bagaimana kita bisa gunakan volume ku bus dalam dapur.
Menggambar Kubus dengan Bantuan Jaring-Jaring
Untuk memudahkan pemahaman siswa, sering kali kita gunakan jaring-jaring kubus, yaitu gambaran 2D dari sisi-sisi ku bus yang jika dilipat membentuk kubus 3D.
Ada banyak variasi jaring-jaring kubus, tapi umumnya terdiri dari 6 persegi yang tersusun secara saling bersentuhan. Melatih menggambar jaring-jaring bisa membantu meningkatkan kemampuan spasial dan imajinasi bentuk ruang anak-anak.
Soal Latihan dan Jawaban
Soal 1:
Sebuah ku bus memiliki rusuk sepanjang 8 cm. Berapa volumenya?
Jawab: V = 8 × 8 × 8 = 512 cm³
Soal 2:
Luas permukaan sebuah ku bus adalah 150 cm². Berapa panjang rusuknya?
Jawab: 6 × s² = 150
s² = 25 → s = 5 cm
Soal 3:
Jika volume ku bus adalah 1000 cm³, berapa panjang rusuknya?
Jawab: s³ = 1000 → s = ∛1000 = 10 cm
Soal semacam ini bisa jadi latihan yang bagus untuk siswa sekaligus penguat pemahaman konsep volume dan luas.
Kesalahan Umum dalam Menghitung Volume Kubus
Beberapa kesalahan umum yang saya temui saat membantu anak belajar:
-
Mengira luas sisi dan volume sama
-
Salah menggunakan rumus (misalnya memakai 6 × s³ untuk volume)
-
Menggunakan satuan tidak konsisten (misalnya rusuk dalam cm, hasil akhir ditulis m³)
Solusinya adalah:
-
Hafalkan rumus pengetahuan dengan logika, bukan sekadar mengingat
-
Gunakan satuan yang seragam
-
Latihan soal kontekstual, bukan hanya angka di kertas
Menghubungkan Konsep Kubus dengan Matematika Lain
Kubus bukan hanya soal geometri. Banyak sekali kaitannya dengan konsep matematika lain:
-
Pangkat tiga (volume = s³)
-
Akar pangkat tiga (untuk mencari panjang rusuk dari volume)
-
Aljabar (kalau variabel digunakan dalam soal kubus)
-
Statistik (menghitung volume ruang penyimpanan data, misalnya di komputer)
Mengintegrasikan konsep ini bisa membantu siswa mengaitkan matematika sebagai satu kesatuan, bukan topik yang berdiri sendiri.
Aplikasi Volume Kubus di Dunia Nyata
Beberapa aplikasi praktis volume kubus:
-
Menghitung daya tampung kolam, kotak, atau wadah
-
Perhitungan pengiriman logistik berdasarkan volume barang
-
Menentukan efisiensi ruang di gudang atau penyimpanan
-
Desain produk industri dan kemasan
-
Simulasi dalam komputer grafik 3D dan game engine
Matematika bukan hanya soal ujian, tapi keterampilan logis yang bisa digunakan di dunia nyata, terutama soal bentuk ruang dan volume.
Penutup: Belajar Kubus Bisa Menyenangkan
Saya percaya bahwa belajar bangun ruang seperti kubus bisa menyenangkan, apalagi jika disampaikan dengan cara yang kontekstual, visual, dan relevan. Anak-anak bisa memahami konsep volume lebih cepat jika diajak langsung menghitung volume dari benda di sekitar mereka.
Rumus boleh jadi bagian penting, tapi pengalaman langsung, logika visual, dan pemahaman konteks akan membuat konsep itu melekat lebih lama. Kubus bukan hanya sekadar bangun ruang, tapi juga jendela awal untuk mengenal dunia matematika secara menyenangkan dan aplikatif.
Baca juga artikel berikut: Persamaan Kuadrat: Rumus dan Trik Mudah Langsung Dapat Akar