JAKARTA, studyinca.ac.id – Dalam dunia statistika, kemampuan menganalisis sebaran data adalah keterampilan fundamental yang wajib dikuasai. Salah satu ukuran letak yang sering digunakan untuk memahami distribusi data adalah kuartil. Rumus Kuartil Data Tunggal menjadi alat penting untuk membagi sekumpulan data menjadi empat bagian sama besar, memberikan gambaran tentang bagaimana nilai-nilai tersebar dalam suatu dataset.
Mahasiswa yang mempelajari statistika dasar pasti akan menemui materi kuartil dalam perkuliahan. Konsep ini tidak hanya berguna untuk keperluan akademis, tetapi juga memiliki aplikasi luas dalam berbagai bidang seperti ekonomi, kesehatan, pendidikan, dan penelitian sosial. Memahami Rumus Kuartil Data Tunggal dengan baik akan memudahkan analisis data di berbagai konteks.
Pengertian Kuartil dalam Statistika
Kuartil adalah nilai-nilai yang membagi sekumpulan data yang telah diurutkan menjadi empat bagian sama besar. Setiap bagian mewakili 25 persen dari keseluruhan data. Dengan demikian, kuartil memberikan informasi tentang posisi relatif suatu nilai dalam distribusi data.
Terdapat tiga nilai kuartil yang membagi data menjadi empat bagian tersebut. Kuartilpertama(Q1) memisahkan 25 persen data terbawah dari 75 persen data sisanya. Kuartil kedua (Q2) sama dengan median yang membagi data menjadi dua bagian sama besar. Kuartil ketiga (Q3) memisahkan 75 persen data terbawah dari 25 persen data teratas.
Karakteristik penting kuartil:
- Q1 disebut kuartil bawah, memotong 25 persen data terendah
- Q2 sama dengan median, memotong 50 persen data
- Q3 disebut kuartil atas, memotong 75 persen data terendah
- Jarak antar kuartil (Q3 minus Q1) disebut Interquartile Range atau IQR
- Kuartil hanya bisa dihitung setelah data diurutkan dari terkecil ke terbesar
- Nilai kuartil tidak harus merupakan anggota data asli
Data tunggal adalah data yang belum dikelompokkan dalam interval kelas. Setiap nilai berdiri sendiri dan biasanya merupakan hasil pengamatan langsung. Rumus Kuartil Data Tunggal berbeda dengan rumus untuk data berkelompok yang sudah disusun dalam tabel distribusi frekuensi.
Rumus Kuartil Data Tunggal
Untuk menghitung kuartil pada data tunggal, langkah pertama yang harus dilakukan adalah mengurutkan data dari nilai terkecil hingga terbesar. Setelah data terurut, posisi kuartil dapat ditentukan menggunakan rumus yang sesuai dengan banyaknya data.
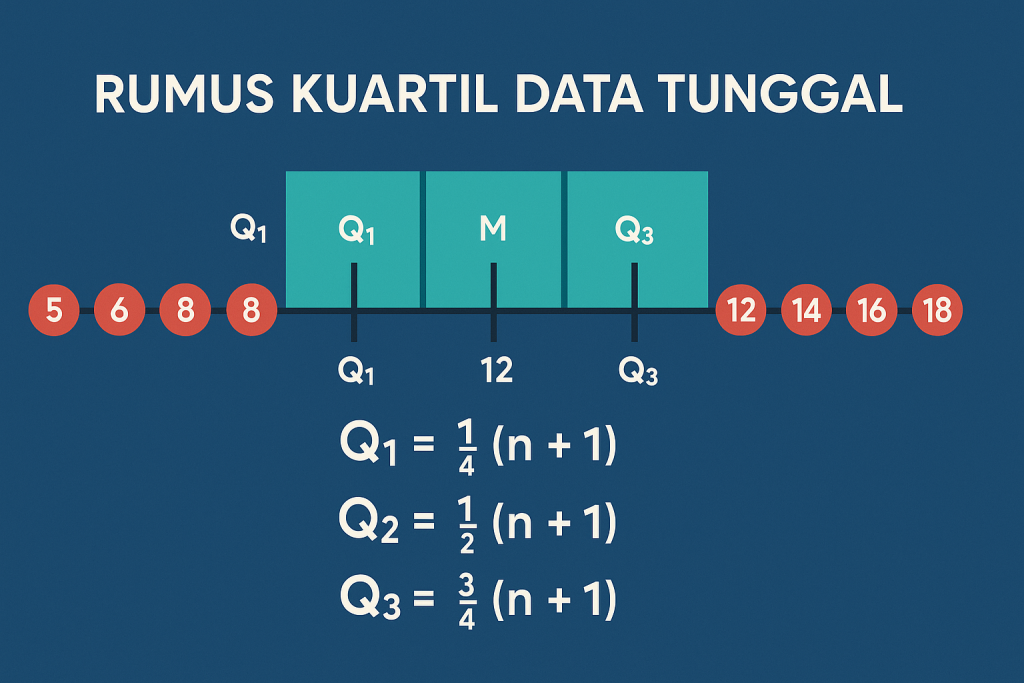
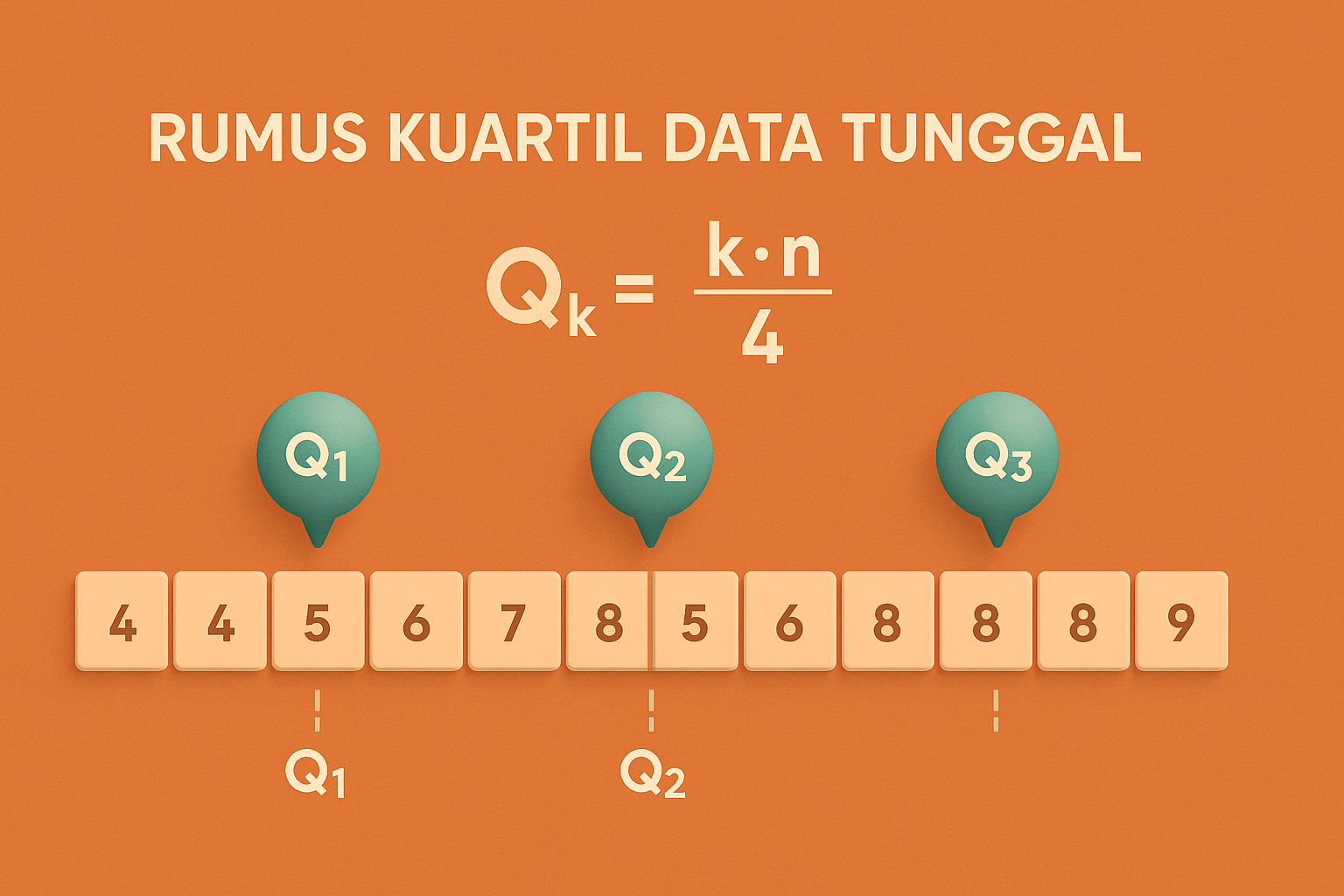
Rumus untuk menentukan letak atau posisi kuartil ke-i pada data tunggal dengan n buah data adalah sebagai berikut. Letak Qi sama dengan i dikali (n + 1) dibagi 4, dimana i adalah 1, 2, atau 3.
Rumus Kuartil Data Tunggal secara lengkap:
- Letak Q1 = (n + 1) / 4
- Letak Q2 = 2(n + 1) / 4 atau (n + 1) / 2
- Letak Q3 = 3(n + 1) / 4
- n adalah banyaknya data dalam dataset
- Hasil letak menunjukkan posisi data ke berapa
Jika hasil perhitungan letak kuartil berupa bilangan bulat, maka nilai kuartil adalah data pada posisi tersebut. Namun jika hasilnya berupa pecahan, diperlukan interpolasi antara dua data yang mengapit posisi tersebut.
Langkah Menghitung Kuartil Data Tunggal
Proses menghitung Rumus Kuartil Data Tunggal memerlukan ketelitian dan urutan langkah yang sistematis. Kesalahan dalam mengurutkan data atau menentukan posisi akan menghasilkan nilai kuartil yang salah.
Langkah pertama adalah mengurutkan seluruh data dari nilai terkecil hingga terbesar. Ini adalah tahap krusial yang tidak boleh dilewatkan. Data yang tidak terurut akan menghasilkan perhitungan kuartil yang keliru.
Tahapan menghitung kuartil data tunggal:
- Urutkan semua data dari nilai terkecil ke terbesar
- Hitung banyaknya data (n)
- Tentukan letak Q1 dengan rumus (n + 1) / 4
- Tentukan letak Q2 dengan rumus 2(n + 1) / 4
- Tentukan letak Q3 dengan rumus 3(n + 1) / 4
- Jika letak berupa bilangan bulat, ambil nilai data pada posisi tersebut
- Jika letak berupa pecahan, lakukan interpolasi linear
- Periksa kembali hasil perhitungan untuk memastikan kebenaran
Interpolasi linear dilakukan ketika letak kuartil jatuh di antara dua data. Misalnya jika letak Q1 adalah 3,25, maka Q1 berada di antara data ke-3 dan data ke-4. Nilai Q1 dihitung dengan menjumlahkan data ke-3 dengan 0,25 dikali selisih data ke-4 dan data ke-3.
Contoh Soal Kuartil Data Tunggal Ganjil
Untuk memahami penerapan Rumus Kuartil Data Tunggal, mari kita lihat contoh soal dengan jumlah data ganjil. Data dengan jumlah ganjil biasanya lebih mudah dihitung karena median jatuh tepat pada satu nilai data.
Diberikan data nilai ujian statistika 11 mahasiswa sebagai berikut: 65, 70, 72, 75, 78, 80, 82, 85, 88, 90, 95. Data ini sudah terurut dari terkecil ke terbesar dengan n = 11.
Perhitungan kuartil untuk data ganjil:
- Letak Q1 = (11 + 1) / 4 = 12 / 4 = 3
- Q1 adalah data ke-3 = 72
- Letak Q2 = 2(11 + 1) / 4 = 24 / 4 = 6
- Q2 adalah data ke-6 = 80
- Letak Q3 = 3(11 + 1) / 4 = 36 / 4 = 9
- Q3 adalah data ke-9 = 88
Interpretasi hasil menunjukkan bahwa 25 persen mahasiswa mendapat nilai di bawah 72, 50 persen di bawah 80, dan 75 persen di bawah 88. Nilai IQR adalah 88 minus 72 sama dengan 16, menunjukkan sebaran 50 persen data tengah.
Contoh Soal Kuartil Data Tunggal Genap
Perhitungan kuartil pada data dengan jumlah genap sedikit berbeda karena posisi kuartil sering jatuh di antara dua data. Dalam kasus ini, interpolasi diperlukan untuk mendapatkan nilai kuartil yang tepat.
Diberikan data tinggi badan 12 siswa dalam sentimeter: 155, 158, 160, 162, 165, 167, 170, 172, 175, 178, 180, 185. Data sudah terurut dengan n = 12.
Perhitungan kuartil untuk data genap:
- Letak Q1 = (12 + 1) / 4 = 13 / 4 = 3,25
- Q1 berada di antara data ke-3 dan ke-4
- Q1 = 160 + 0,25 × (162 – 160) = 160 + 0,5 = 160,5 cm
- Letak Q2 = 2(12 + 1) / 4 = 26 / 4 = 6,5
- Q2 = 167 + 0,5 × (170 – 167) = 167 + 1,5 = 168,5 cm
- Letak Q3 = 3(12 + 1) / 4 = 39 / 4 = 9,75
- Q3 = 175 + 0,75 × (178 – 175) = 175 + 2,25 = 177,25 cm
Hasil perhitungan menunjukkan bahwa Q1 = 160,5 cm, Q2 = 168,5 cm, dan Q3 = 177,25 cm. Perhatikan bahwa nilai kuartil hasil interpolasi bukan merupakan anggota data asli.
Contoh Soal dengan Pembahasan Lengkap
Untuk memperdalam pemahaman tentang Rumus Kuartil Data Tunggal, berikut contoh soal yang lebih kompleks dengan pembahasan tahap demi tahap.
Soal: Data pengeluaran bulanan 15 keluarga dalam jutaan rupiah adalah: 4,5; 3,2; 5,8; 2,9; 6,5; 4,1; 3,8; 5,2; 7,0; 4,8; 3,5; 6,2; 5,5; 4,0; 5,0. Tentukan Q1, Q2, Q3, dan IQR.
Langkah penyelesaian:
- Urutkan data: 2,9; 3,2; 3,5; 3,8; 4,0; 4,1; 4,5; 4,8; 5,0; 5,2; 5,5; 5,8; 6,2; 6,5; 7,0
- Banyak data n = 15
- Letak Q1 = (15 + 1) / 4 = 4, maka Q1 = data ke-4 = 3,8 juta
- Letak Q2 = 2(15 + 1) / 4 = 8, maka Q2 = data ke-8 = 4,8 juta
- Letak Q3 = 3(15 + 1) / 4 = 12, maka Q3 = data ke-12 = 5,8 juta
- IQR = Q3 – Q1 = 5,8 – 3,8 = 2,0 juta
Interpretasi: Sebanyak 25 persen keluarga memiliki pengeluaran di bawah 3,8 juta, median pengeluaran adalah 4,8 juta, dan 75 persen keluarga memiliki pengeluaran di bawah 5,8 juta. Rentang 50 persen data tengah adalah 2 juta rupiah.
Interpretasi Hasil Kuartil
Menghitung kuartil saja tidak cukup tanpa kemampuan menginterpretasikan hasilnya dengan benar. Rumus Kuartil Data Tunggal menghasilkan nilai-nilai yang memiliki makna statistik penting dalam analisis data.
Q1 memberikan informasi tentang batas bawah data. Nilai di bawah Q1 termasuk dalam 25 persen terendah. Dalam konteks nilai ujian, siswa dengan nilai di bawah Q1 bisa dianggap berada di kelompok bawah yang mungkin memerlukan perhatian khusus.
Makna interpretasi kuartil:
- Data di bawah Q1 termasuk 25 persen terendah dari seluruh data
- Data antara Q1 dan Q2 termasuk 25 persen berikutnya
- Data antara Q2 dan Q3 termasuk 25 persen di atas median
- Data di atas Q3 termasuk 25 persen tertinggi
- IQR menunjukkan sebaran atau variabilitas 50 persen data tengah
- IQR kecil menandakan data cenderung homogen
- IQR besar menandakan data cenderung heterogen
Dalam analisis outlier, kuartil sangat berguna. Data yang nilainya kurang dari Q1 – 1,5 × IQR atau lebih dari Q3 + 1,5 × IQR sering dianggap sebagai outlier atau pencilan yang perlu perhatian khusus dalam analisis.
Perbedaan Kuartil Data Tunggal dan Data Kelompok
Penting untuk membedakan Rumus Kuartil Data Tunggal dengan rumus untuk data kelompok. Keduanya memiliki pendekatan perhitungan yang berbeda meskipun konsep dasarnya sama.
Data tunggal adalah data mentah yang belum dikelompokkan dalam interval kelas. Setiap observasi tercatat sebagai nilai individual. Sementara data kelompok sudah disusun dalam tabel distribusi frekuensi dengan interval kelas tertentu.
Perbedaan utama perhitungan kuartil:
- Data tunggal menggunakan rumus letak Qi = i(n + 1) / 4
- Data kelompok menggunakan rumus yang melibatkan tepi bawah kelas dan frekuensi
- Data tunggal menghasilkan nilai pasti atau hasil interpolasi sederhana
- Data kelompok menghasilkan nilai perkiraan dalam suatu interval
- Data tunggal cocok untuk dataset berukuran kecil hingga sedang
- Data kelompok lebih efisien untuk dataset berukuran sangat besar
- Akurasi data tunggal lebih tinggi karena menggunakan nilai sebenarnya
Dalam praktik penelitian, pemilihan metode tergantung pada bagaimana data dikumpulkan dan disajikan. Jika data tersedia dalam bentuk mentah, gunakan Rumus Kuartil Data Tunggal untuk hasil yang lebih akurat.
Aplikasi Kuartil dalam Kehidupan Nyata
Pemahaman Rumus Kuartil Data Tunggal tidak hanya berguna dalam konteks akademis. Berbagai bidang memanfaatkan kuartil untuk analisis dan pengambilan keputusan berbasis data.
Dalam dunia pendidikan, kuartil digunakan untuk menentukan ranking dan klasifikasi prestasi siswa. Siswa di kuartil atas (di atas Q3) bisa diidentifikasi sebagai berprestasi tinggi, sementara yang di bawah Q1 mungkin memerlukan bimbingan tambahan.
Penerapan kuartil di berbagai bidang:
- Pendidikan: klasifikasi prestasi dan penentuan program remedial
- Ekonomi: analisis distribusi pendapatan dan kesenjangan
- Kesehatan: standar pertumbuhan anak dan indikator kesehatan
- Keuangan: analisis kinerja portofolio dan manajemen risiko
- SDM: evaluasi kinerja karyawan dan penentuan kompensasi
- Penelitian: identifikasi outlier dan analisis sebaran data
- Pemasaran: segmentasi pelanggan berdasarkan perilaku belanja
Di bidang kesehatan, grafik pertumbuhan anak menggunakan persentil yang konsepnya mirip dengan kuartil. Dokter membandingkan berat atau tinggi badan anak dengan persentil populasi untuk menilai status pertumbuhan.
Tips Menghindari Kesalahan Perhitungan
Dalam menerapkan Rumus Kuartil Data Tunggal, beberapa kesalahan umum sering terjadi. Mengetahui kesalahan-kesalahan ini membantu menghindarinya dan menghasilkan perhitungan yang akurat.
Kesalahan paling umum adalah lupa mengurutkan data sebelum menghitung. Rumus kuartil hanya berlaku untuk data yang sudah terurut dari terkecil ke terbesar. Menerapkan rumus pada data acak akan menghasilkan nilai yang tidak bermakna.
Kesalahan umum dan cara menghindarinya:
- Tidak mengurutkan data: selalu urutkan data sebelum menghitung
- Salah menentukan n: hitung ulang jumlah data dengan teliti
- Kesalahan interpolasi: perhatikan posisi desimal dengan cermat
- Menggunakan rumus data kelompok: pastikan jenis data yang digunakan
- Salah membaca posisi: verifikasi urutan data setelah pengurutan
- Tidak memeriksa hasil: bandingkan nilai kuartil dengan logika distribusi data
Verifikasi hasil adalah langkah penting yang sering diabaikan. Nilai Q1 harus selalu lebih kecil dari Q2, dan Q2 harus lebih kecil dari Q3. Jika hasil tidak memenuhi syarat ini, pasti ada kesalahan dalam perhitungan.
Penutup
Rumus Kuartil Data Tunggal adalah alat statistik fundamental yang wajib dikuasai oleh mahasiswa dan praktisi yang bekerja dengan data. Kemampuan menghitung dan menginterpretasikan kuartil membuka jalan untuk analisis data yang lebih kompleks seperti box plot dan deteksi outlier.
Kunci keberhasilan dalam menghitung kuartil adalah ketelitian dalam mengurutkan data, ketepatan dalam menerapkan rumus, dan kemampuan melakukan interpolasi ketika diperlukan. Dengan latihan yang cukup, perhitungan kuartil akan menjadi keterampilan yang dapat dilakukan dengan cepat dan akurat, memberikan insight berharga tentang karakteristik distribusi data yang sedang dianalisis.
Baca juga konten dengan artikel terkait tentang: Pengetahuan
Baca juga artikel lainnya: Perkalian Silang: Pengertian, Cara Hitung, dan Contoh